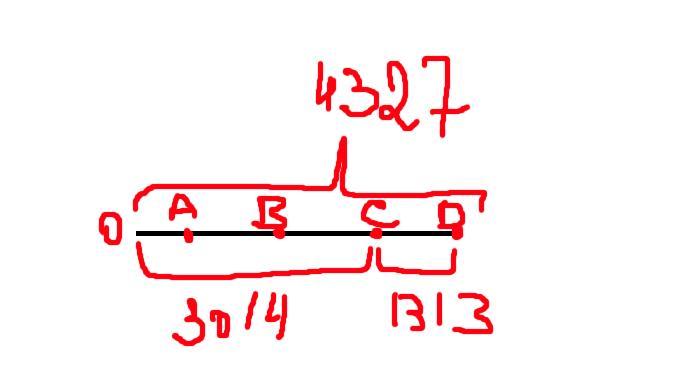
велосипедист проехал 4327
и останавливаясь в четырёх
разных пунктах.
найти самый
короткий отрезок
дороги, если самый
длинный был
1313 м.
Ответы
Ответ:
390м
Пошаговое объяснение:
Если весь путь 4327 и самый длинный из этого 1313, то вычтем из всего пути, самый длинный путь.
4327-1313 = 3014
Начало движения велосипедиста за пункт остановки не считаем, считаем за пункт остановки только самый последний и 3 других.
Пусть 1313 м это был самый последний участок дороги.
Для удобства обозначим пункты остановки ABCD, CD = 1313
Пусть точка начала движения будет точка О.
Можем составить уравнение, для удобства.
Пусть ОА = x, АB = y, BC = z
x+y+z=3014
По условиям задачи не дано соотношения дороги, значит мы можем проявить фантазию. Пусть OA будет 1.
Тогда, 1+y+z=3014
Получается AB=BC
Значит
1+2y=3014
2y=3013
y=1506,5, не подходит по условию задачи, т.к. самый длинный отрезок
1313м. Прикинем примерное число, что бы 2y=3014-x <1313
Пусть x=400м, тогда 2y=2614, а y=1307, уже подходит под условие задачи. 1307<1313, попробуем выбрать такое число, которое будет максимально приближено к 1313. Это число 1312
Получается, при x = 394 y= 1310
При x = 392 y=1311
А при x = 390 y = 1312, что нам подходит.
Значит, отрезок ОА=390 метров AB=1312 BC=1312 CD=1313, проверим
390+1312+1312+1313 = 4327, значить 390 метров самый короткий отрезок