Предмет: Алгебра,
автор: pinkiecake
Исследовать на экстремумы функцию
Приложения:
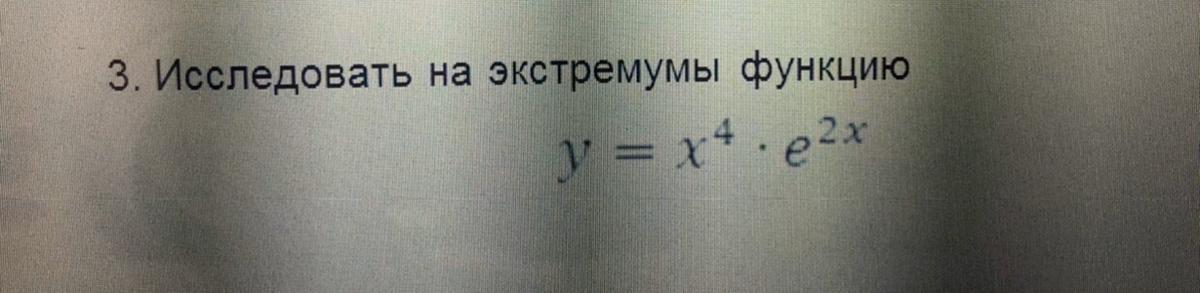
Ответы
Автор ответа:
1
Ответ:
0, -2
Объяснение:
Дифференцируем уравнение, то есть находим производную. Затем приравниваем её к нулю, чтобы найти экстремумы
Разделим на , так как эта величина не равна нулю. Получаем:
Если , это будет решением уравнения. Иначе разделим уравнение на
. Получаем:
. Получили вторую точку экстремума - это
. Так как функция при стремлении x к бесконечности стремится к бесконечности, то в x = 0 -- её локальный минимум, в x = -2 -- её локальный максимум
Похожие вопросы
Предмет: Українська мова,
автор: Валидол2012
Предмет: Русский язык,
автор: andrian2003
Предмет: Українська мова,
автор: asya28
Предмет: Математика,
автор: mikhail8115