Question

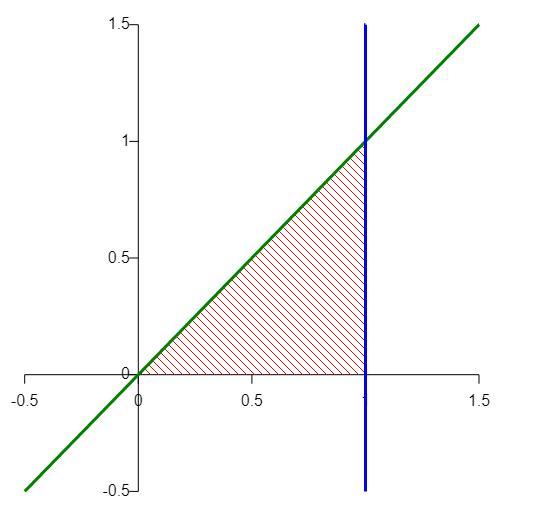
Вычислить двойной интеграл по области D.
Область D ограничена линиями: y = 0; y = x; x = 1
(x^2+5y)dx dy

Answer 1

Область інтегрування дивіться на малюнку. Будуємо графіки і знаходимо цю область. Тому далі вичислимо подвійний інтеграл.

$\displaystyle \iint_D\Big(x^2+5y\Big)dxdy=\int\limits^1_0dy\int\limits^1_y\Big(5y+x^2\Big)dx=\int\limits^1_0\Bigg(5xy+\dfrac{x^3}{3}\Bigg)\bigg|^1_ydy=\\ \\ \\ =\int\limits^1_0\Bigg(5y+\dfrac{1}{3}-5y^2-\dfrac{y^3}{3}\Bigg)dy=\Bigg(\dfrac{5y^2}{2}+\dfrac{y}{3}-\dfrac{5y^3}{3}-\dfrac{y^4}{12}\Bigg)\bigg|^1_0=\\ \\ \\ =\dfrac{5}{2}+\dfrac{1}{3}-\dfrac{5}{3}-\dfrac{1}{12}=\dfrac{13}{12}$