Question

Геометрия!!! 100 баллов

4. Шар пересечен параллельными плоскостями, расположенными по разные стороны от центра шара. Площадь большего сечения составляет 1 целая 7/9 площади меньшего сечения. Вычислите расстояние между секущими плоскостями, если длина радиуса шара равна 10 см, а площадь большего сечения равна 64π см²
​

Answer 1

Ответ:

14 см

Объяснение:

Пусть S₁ - площадь большего сечения, S₂ - площадь меньшего сечения

r₁ - радиус большего сечения, r₂ - радиус меньшего сечения

$S_1 = \frac{16}{9}S_2 \Rightarrow S_2 = \frac{9}{16}S_1 \\ \\ S_2 = \frac{9}{16}\cdot 64\pi = 36\pi$

$S_1 = 64\pi ~cm^2\\ \\ S_1 = \pi r_1^2 \\ \\ \pi r_1^2 = 64 \pi \Rightarrow r_1 = 8~ cm$

$S_2 = 36 \pi~ cm^2 \\ \\ S_2 = \pi r_2^2 \\ \\ \pi r_2^2 = 36 \pi \Rightarrow r_2 = 6~ cm$

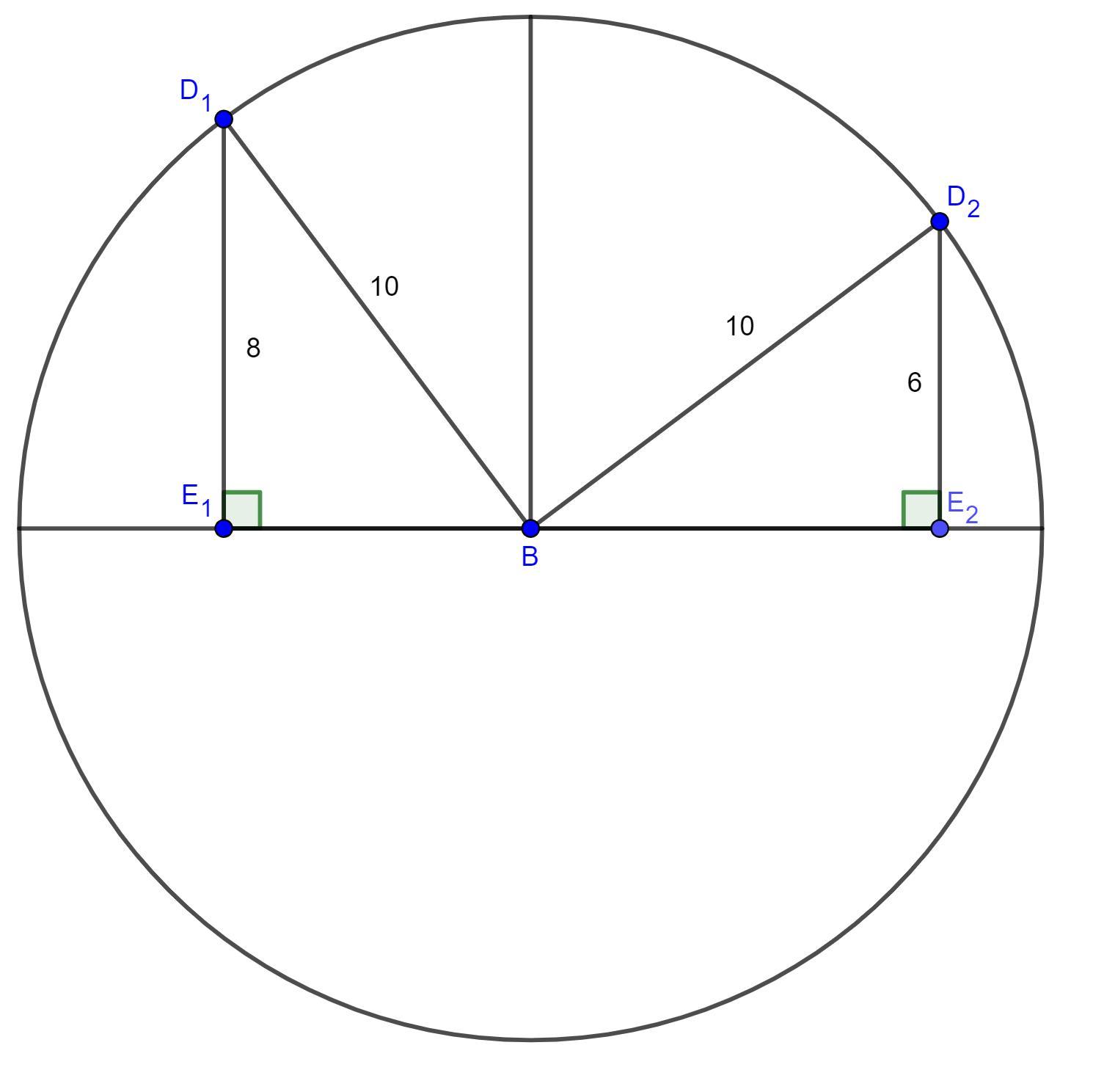
В приложении изображение осевого сечения шара.

По условию, плоскости, пересекающие шар, расположены по разные стороны от его центра.

Рассмотрим ΔBD₁E₁ - прямоугольный, BD₁ = 10 см - радиус шара, D₁E₁ = 8 см - радиус большего сечения

Найдём BE₁ по теореме Пифагора

$BE_1^2 = BD_1^2 - D_1E_1^2 \\ \\ BE_1^2 = 10^2 - 8^2 = 36 \\ \\ BE_1 = 6~ cm$

Рассмотрим ΔBD₂E₂ - прямоугольный, BD₂ = 10 см - радиус шара, D₂E₂ = 6 см -  радиус меньшего сечения

Найдём BE₂ по теореме Пифагора

$BE_2^2 = BD_2^2 - D_2E_2^2 \\ \\ BE_2^2 = 10^2 - 6^2 = 64 \\ \\ BE_2 = 8 ~cm$

Расстояние между плоскостями  равно длине отрезка E₁E₂

E₁E₂ = E₁B + BE₂ = 8 + 6 = 14 см