Question

ГЕОМЕТРИЯ!!! 100 баллов

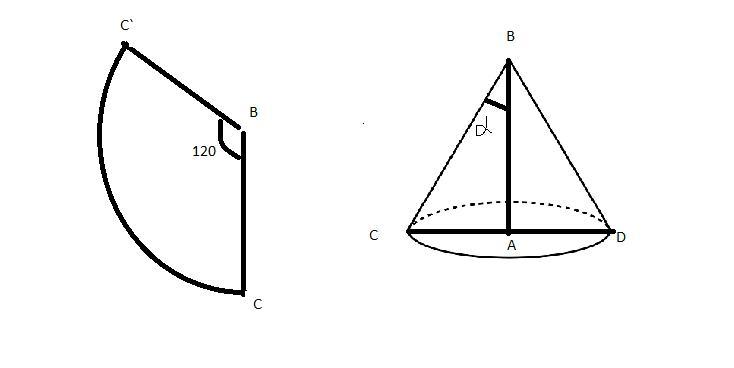
5. Развертка боковой поверхности конуса – сектор с центральным углом 120°. Найдите объем конуса, если периметр его осевого сечения равен 16 см.​

Answer 1

∠φ = 360° * sinα

Используя данный нам ∠φ (угол развертки боковой поверхности, равен 120°) найдем sinα

120° = 360° * sinα

sinα = 1/3

Рассмотрим Δ BDC-осевое сечение конуса

Р (ΔBDC )= 16 см

СА=АD

СА = 2R

Р( ΔBDC0 = 2L + 2R (L-образующая конуса)

16 = 2L + 2R

8 = L + R

L = 8 - R

Перейдем к прямоугольному Δ АВС. ∠ВАС = 90°, АС = R

ВС = 8 - R

sinα = AC/CB = R/(8 - R)

R/(8 - R) = 1/3

3R = 8 - R

4R = 8

R = 2

L=8-2=6

h^2=L^2-R^2=6^2-2^2=36-4=32

h=4√2

V=piR^2*h/3=pi*2^2*4√2/3=16√2/3