Предмет: Геометрия,
автор: slsld
В кубе abcda1b1c1d1 ребро равно 2а .через середину ребра CD проведена плоскость параллельная плосткости BC1D . Найдите площадь сечения
логичное решение
20 баллов
Ответы
Автор ответа:
0
Ответ:
S = (√3/2)·а² ед².
Объяснение:
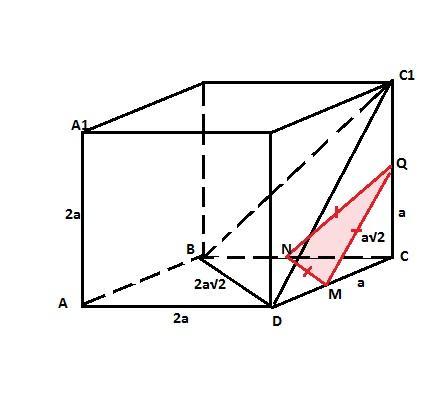
Пусть середина ребра CD - точка М. Плоскость, проходящая через эту точку и параллельная плоскости BC1D - это плоскость MNQ со сторонами MN║BD, MQ║DC1 и NQ║BC1, которые являются средними линиями треугольников CBD, CDC1 и СВС1 соответственно. Значит они равны половине диагонали грани куба со стороной 2а, то есть равны а·√2.
Итак, искомое сечение - равносторонний треугольник со стороной, равной а√2.
Его площадь равна по формуле: S = (√3/4)·(a√2)² =(√3/2)·а²
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: KaterinkaMilKa
Предмет: Английский язык,
автор: XAndreiX
Предмет: Другие предметы,
автор: Valek1997
Предмет: Алгебра,
автор: timanna2000
Предмет: Математика,
автор: чик12