Question

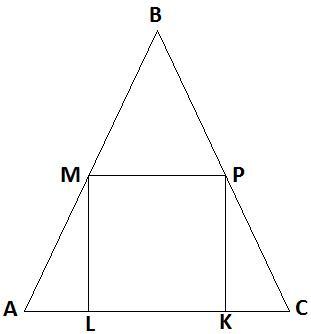
52 БАЛЛА! ПОМОГИТЕ! В равносторонний треугольник АВС со стороной АВ = 1 см вписан квадрат KLMP, как показано на рисунке. Найдите сторону квадрата.

Answer 1

Ответ: √3:(2+√3) или, иначе, 2√3-3

Объяснение: Примем сторону квадрата равной х. Стороны квадрата попарно равны и параллельны.

Следовательно, углы при МР и АС равны,  ∆ ВМР подобен ∆ АВС - он правильный, поэтому ВМ=МР=х

В прямоугольном ∆ АМL  гипотенуза АМ=АВ-ВМ=1-х

АL=ML:tg60°=x:√3

С другой стороны, АL=AM•cos60° =>

x/√3=(1-x)•1/2 =>

2x=√3-x√3 =>

2x+x√3=√3 =>

x•(2+√3)=√3, откуда х=√3:(2+√3).

Умножив числитель и знаменатель получившейся дроби на (2-√3), получим √3(2-√3):(4-3)=2√3-3

------------------

Можно применить т.Пифагора из того же треугольника и получить  тот же результат, или подобие треугольников АВН ( ВН - высота) и АМL, так как в подобных треугольниках отношение катетов одного из них равно отношению катетов другого.