Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить !!!
Приложения:
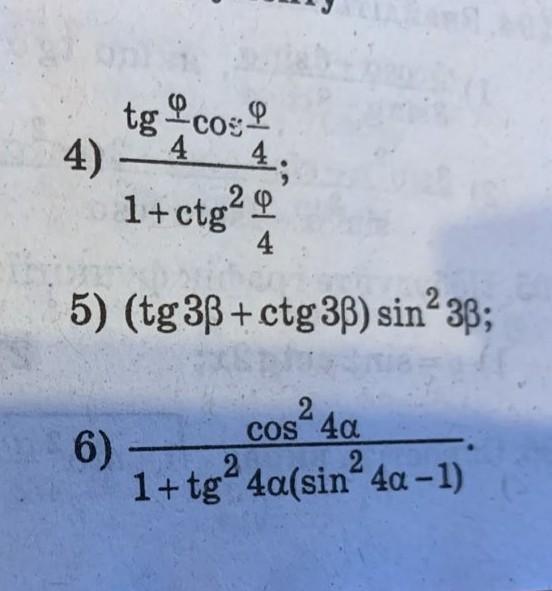
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: zorig
Предмет: Русский язык,
автор: Гулназочка
Предмет: Русский язык,
автор: КатяЛена
Предмет: Физика,
автор: polinakarataev
Предмет: Информатика,
автор: pux228