Предмет: Математика,
автор: mRqus226
Типовой расчёт,помогите!
Приложения:
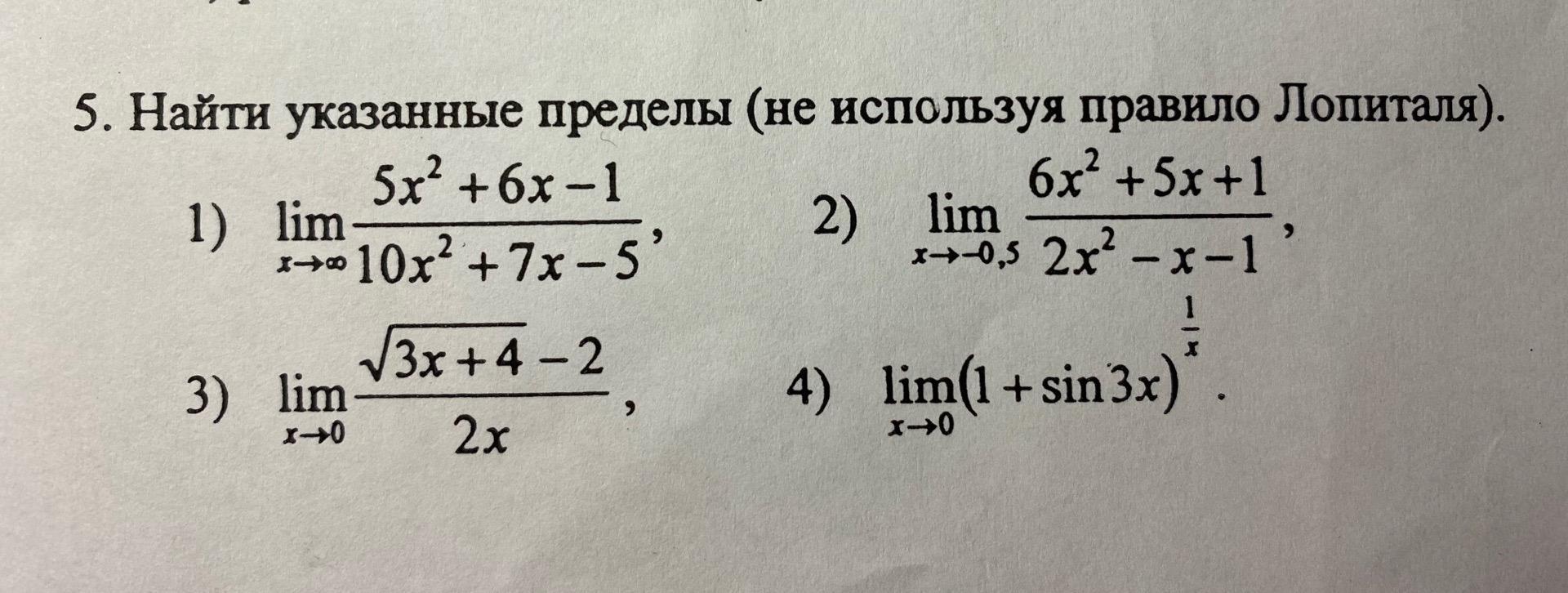
Ответы
Автор ответа:
1
Пошаговое объяснение:
1)
2)
3) 4)
По второму замечательному пределу:
По первому замечательному пределу:
Похожие вопросы
Предмет: Другие предметы,
автор: Janiffer
Предмет: Русский язык,
автор: Алексей200
Предмет: Английский язык,
автор: SFrost
Предмет: История,
автор: ник3842
Предмет: Математика,
автор: Aluina10