Question

Найдите количество корней уравнения $1+ctgx=cosx+\frac{1}{sinx}$ , принадлежащих отрезку [0°; 360°]

Answer 1

Котангенс - это отношение косинуса к синусу, тогда:

$1+\frac{cosx}{sinx}=cosx+\frac{1}{sinx}$

$\frac{sinx+cosx-sinxcosx-1}{sinx} =0$

ОДЗ:

sinx ≠ 0

х ≠ Пn

sinx + cosx - sinxcosx - 1 = 0

sinx (1 - cosx) - (1 - cosx) = 0

(1 - cosx) (sinx - 1) = 0

[ 1 - cos x = 0 ⇒ [ cosx = 1 ⇒ [ x = 2Пn   n ∈ z

[ sinx - 1 = 0  ⇒  [ sinx = 1 ⇒ [ x = п/2 + 2Пn   n ∈ z

Подставляем под ОДЗ:

x = п/2 + 2Пn, n ∈ z

Наш промежуток, переводя в пи будет выглядеть следующим образом:

[0°; 2п]

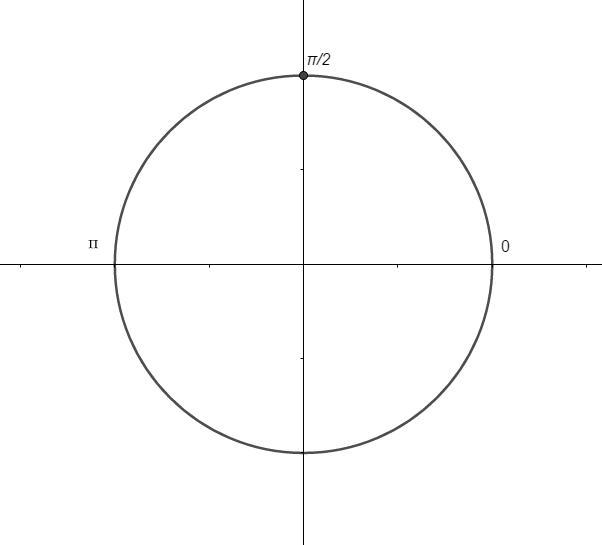
Т.е, это целый оборот круга. Я в приложении представил нашу окружность с указанной на ней точкой ответа.

Ответ: Данному отрезку принадлежит один корень: п/2