Предмет: Алгебра,
автор: sasha1507
Найдите сумму целых решений неравенства 
Ответы
Автор ответа:
1
Ответ:
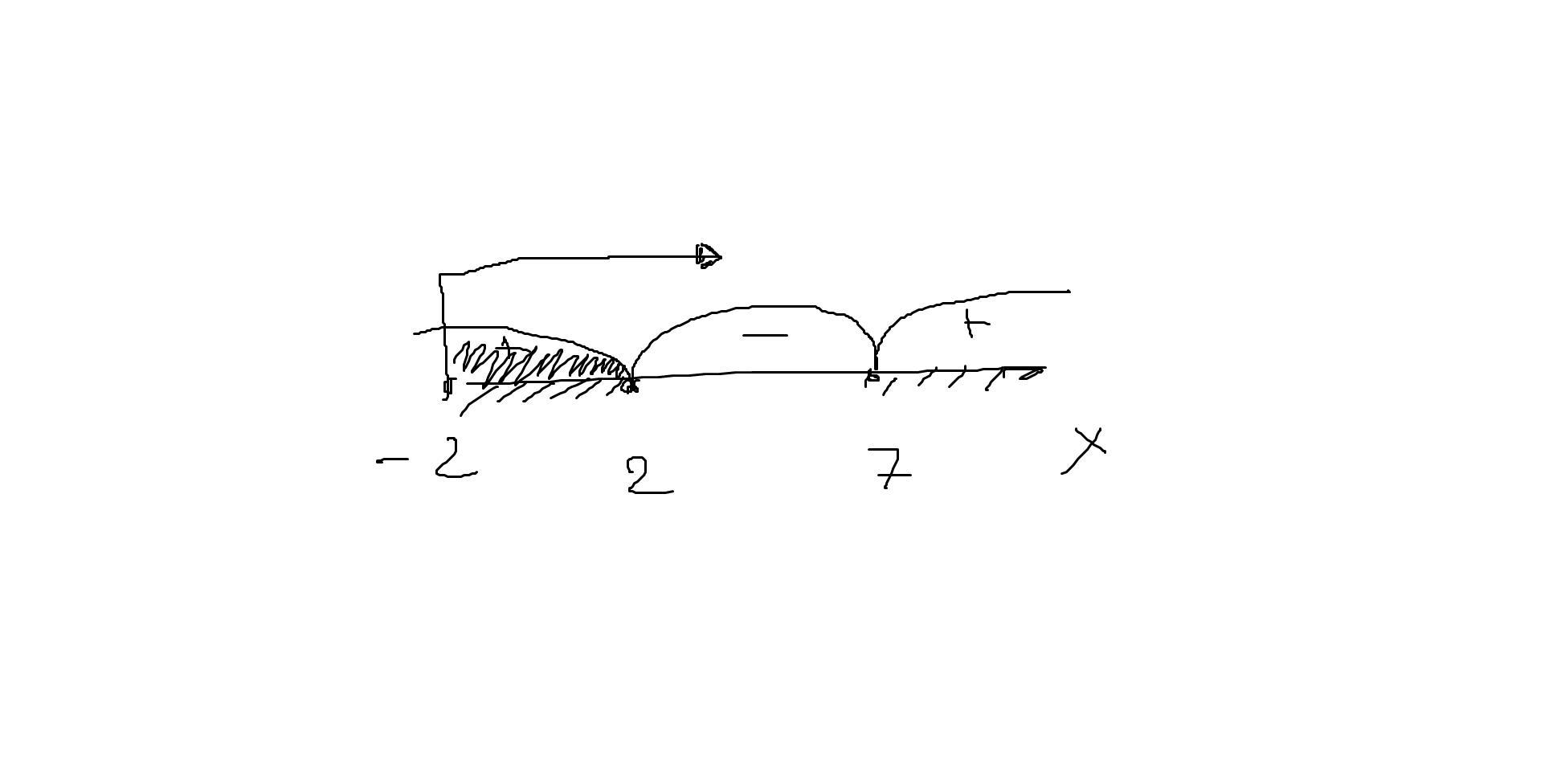
Получаем ответ : x∈[-2;2]
Объяснение:
Ну тут же все ясно. Сначала следует найти ОДЗ(Область Допустимых Значений), которая равна : ->
(из свойства четной степени корня). Оставив на время ОДЗ, возводим в квадрат обе части :
Преобразуем :
Переносим все в правую часть:
Находим корни уравнения:
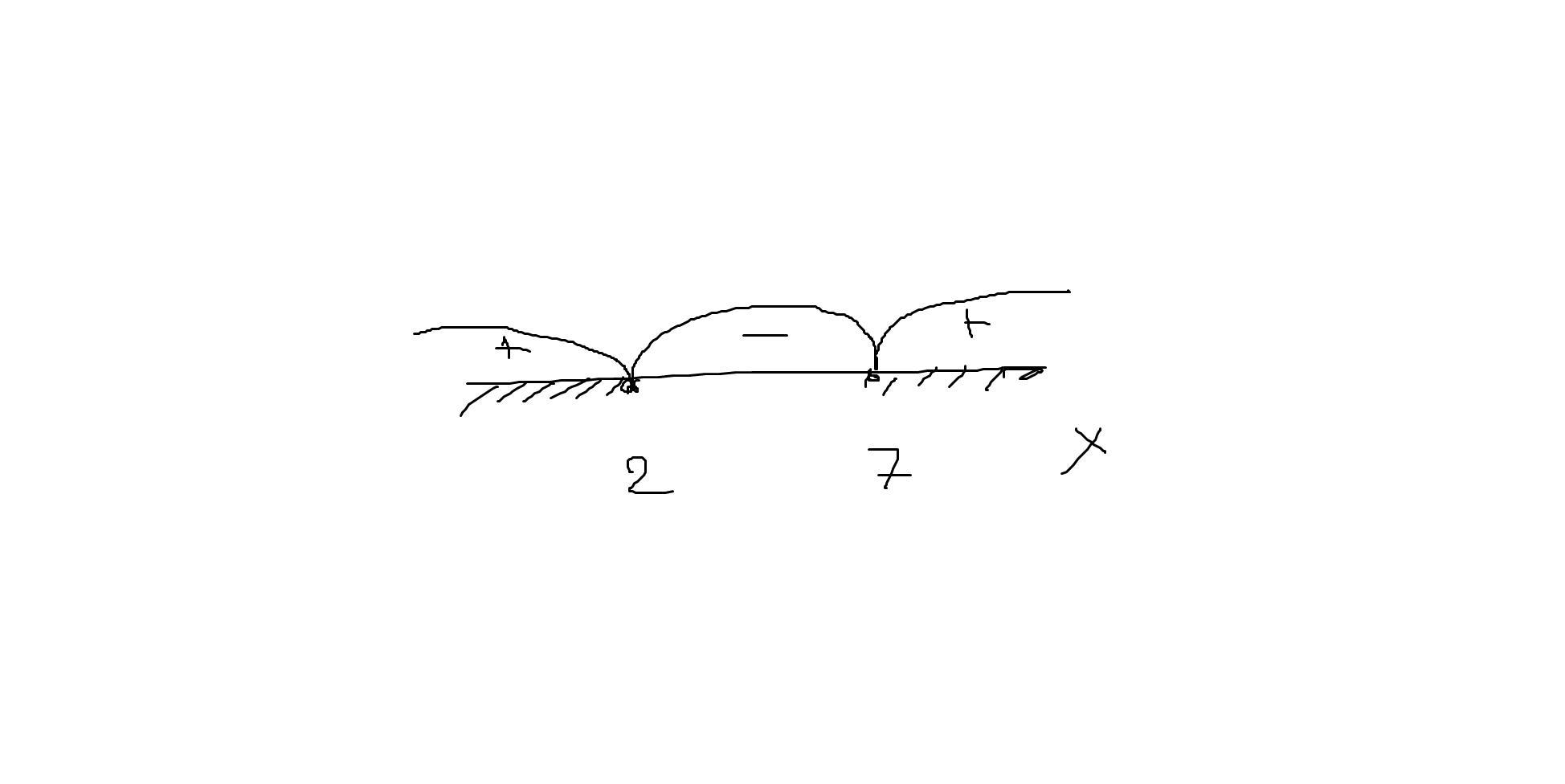
Находим решение для квадратного уравнения методом интервалов:
https://ru-static.z-dn.net/files/d93/71e9c0394c87e3db433678f89499dbb5.png
Пишем решение кв. ур. :
x∈(-∞;2]∪[7;+∞)
Совместим решение с ОДЗ:
https://ru-static.z-dn.net/files/d69/80e658e1a101b95b7e4d288ed85d51b8.png
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: kate55
Предмет: Английский язык,
автор: ugolek
Предмет: Математика,
автор: ббэшка
Предмет: Биология,
автор: НастяNM