Предмет: Математика,
автор: blackswan1306
объясните, пожалуйста, как решать
Приложения:
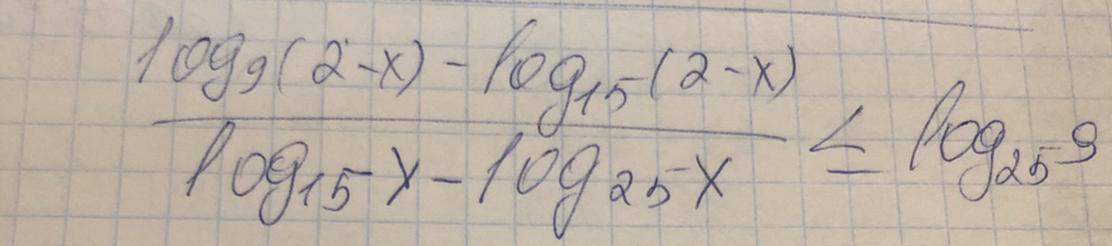
Ответы
Автор ответа:
1
Прежде всего, найдем ОДЗ:
Следовательно,
Преобразуем левую часть неравенства:
Решим неравенство методом интервалов.
Данное равенство будет выполняться, если
Следовательно, . Однако, этот корень не входит в ОДЗ. Значит, уравнение не имеет решений.
Итог: данное неравенство будет выполнятся всегда или не выполнится никогда. Проверим это, подставив любую точку из ОДЗ, например,
— истина.
Следовательно, данное неравенство выполняется при всех из области определения.
Ответ:
ой я поняла
спасибо за решение)
спасибо за решение)
Пожалуйста!
а мне поможете? пожалуйста. https://znanija.com/task/34262649 тут.
Похожие вопросы
Предмет: Английский язык,
автор: Mashirik
Предмет: Другие предметы,
автор: Diinar
Предмет: Русский язык,
автор: galigo
Предмет: Математика,
автор: РоманСМ
Предмет: Математика,
автор: АйданаЖуматаева38
и да, спасибо огромное