Предмет: Математика,
автор: tanya15t1
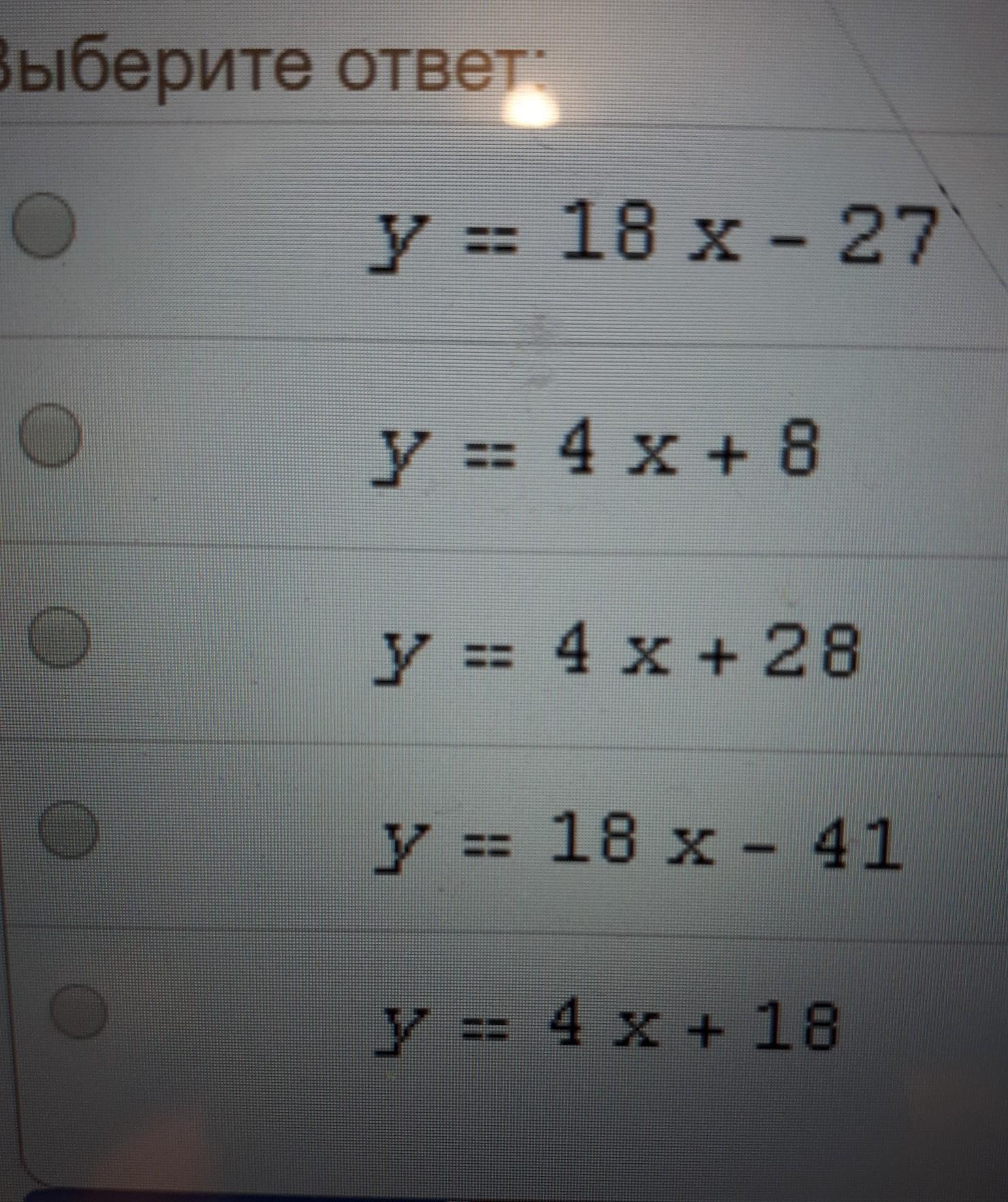
составьте уравнение касательной к графику функции

в точке с абсциссой

Варианты на фото
Приложения:
Reideen:
у=4х+8
Ответы
Автор ответа:
1
Ответ: y=4x+8
Похожие вопросы
Предмет: Русский язык,
автор: mail1996
Предмет: Русский язык,
автор: Dasha604
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: woilo2016