Question

допоможіть будь ласка !!!
9 клас ❤

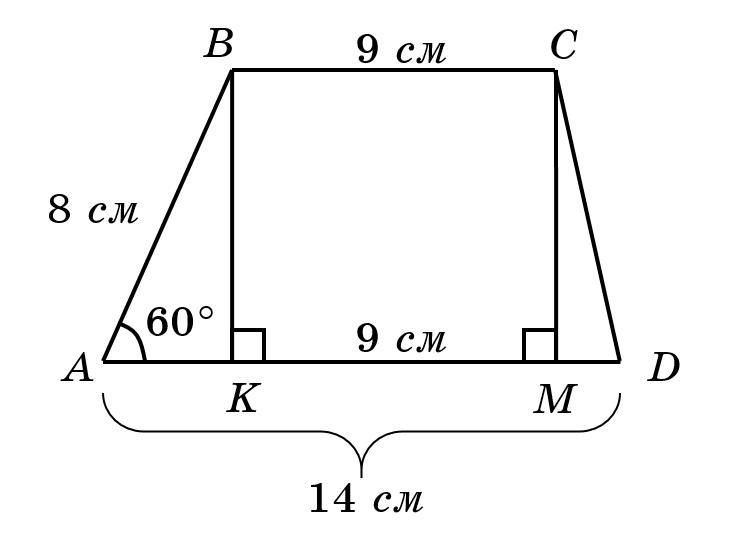
у трапеції ABCD основи BC і AD дорівнюють відповідно 9 см і 14 см, а АВ=8 см. знайдіть CD, якщо кут А = 60°.​

Answer 1

Нехай є трапеція $ABCD$ з основами $AD = 14$ см та $BC = 9$ см й боковою стороною $AB = 8$ см, $\angle A = 60^{\circ}$ (см. рисунок).

Треба знайти $CD$.

Опустимо два перпендикуляри (висоти) $BK$ і $CM$.

Розглянемо прямокутний трикутник $ABK \ (\angle K = 90^{\circ}):$

$\sin \angke A = \dfrac{BK}{AB} \Rightarrow \dfrac{\sqrt{3}}{2} = \dfrac{BK}{8} \Rightarrow BK = 4\sqrt{3}$ см. Відповідно $CM = 4\sqrt{3}$ см.

$\cos \angle A = \dfrac{AK}{AB} \Rightarrow \dfrac{1}{2} = \dfrac{AK}{8} \Rightarrow AK = 4$ см.

У прямокутнику $KBCM$ сторони $BC$ і $KM$ рівні та дорівнюють 9 см. Отже, відрізок $MD = AD - (AK + KM) = 14 - (4 + 9) = 1$ см.

Розглянемо прямокутний трикутник $CMD \ (\angle M = 90^{\circ}):$

За теоремою Піфагора $CD = \sqrt{CM^{2} + MD^{2}}= \sqrt{(4\sqrt{3})^{2} + 1^{2}} = \sqrt{49} = 7$ см.

Відповідь: 7 см.