Question

Докажите ,что если один из углов прямоугольного треугольника равен 30 ,то катет,лежащий против этого угла,равен половине гипотенузы​

Answer 1

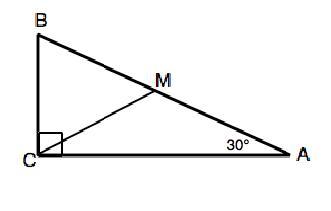
Пусть в прямоугольном треугольнике АВС угол А=30°, угол С=90°. Сумма острых углов прямоугольного треугольника 90°, поэтому угол В=90°-30°=60°

 Проведем из прямого угла отрезок СМ так, что угол МСВ=60°.

Тогда в ∆ ВСМ угол СМВ=180°-угол АСВ-угол МВС=180°-2•60°=60°. Углы ∆ВСМ равны, это треугольник равносторонний по определению. ВС=ВМ=СМ.

  В ∆ АСМ угол АСМ=90°-60°=30°. Т.к. углы при основании АС равны, то ∆ АМС - равнобедренный по определению, АМ=СМ.

Но СМ=ВМ => АМ=ВМ=ВС. =>

АВ=2ВС, , т.е. катет ВС, противолежащий углу 30°, равен половине гипотенузы, что и требовалось доказать.