Question

помогите решить, пожалуйста!

Answer 1

$1a)\; \; 2x^2-x=0\; ,\; x(2x-1)=0\; ,\; x_1=0\; ,\; x_2=\frac{1}{2}\\\\b)\; \; 9-x^2=0\; ,\; (3-x)(3+x)=0\; ,\; \; x_1=3\; ,\; \; x_2=-3\\\\c)\; \; 2x^2-x-1=0\; ,\; \; D=9\; ,\; \; x_1=\frac{1-3}{4}=-\frac{1}{2}\; ,\; \; x_2=\frac{1+3}{4}=1\\\\d)\; \; \frac{x^2}{x+6}=1\; ,\; \; \frac{x^2-x-6}{x+6}=0\; ,\; \; \left \{ {{x^2-x-6=0} \atop {x\ne -6}} \right.\; \; \left \{ {{D=25\; ,\; x_1=-2\; ,\; x_2=3} \atop {x\ne -6\qquad \qquad \quad }} \right.\; \to \\\\x_1=-2\; ,\; x_2=3$

$e)\; \; \frac{x^2+2x}{x-1}=\frac{3}{x-1}\; ,\; \; \left \{ {{x^2+2x=3} \atop {x\ne 1}} \right.\; \; \left \{ {{x^2+2x-3=0} \atop {x\ne 1}} \right.\; \; \left \{ {{x_1=-3\; ,\; x_2=1} \atop {x\ne 1\qquad \quad }} \right.\; \to \; \; x=-3\\\\f)\; \; \frac{5}{x+1}+\frac{4}{x-2}=\frac{3}{x-3}\; ,\; \; \frac{5(x-2)(x-3)+4(x+1)(x-3)-3(x+1)(x-2)}{(x+1)(x-2)9x-3)}=0\\\\\frac{5(x^2-5x+6)+4(x^2-2x-3)-3(x^2-x-2)}{(x+1)(x-2)(x-3)}=0\; ,\; \; \frac{6x^2-30x+24}{(x+1)(x-2)(x-3)}=0\; ,$

$\left \{ {{6x^2-30x+24=0} \atop {x\ne -1,\; x\ne2,\; x\ne 3}} \right.\; \; \left \{ {{x^2-5x+4=0} \atop {x\ne -1,\; x\ne2,\; x\ne 3}} \right.\; \; \left \{ {{x_1=1,\; x_2=4} \atop {x\ne -1,\; x\ne 2,\; x\ne 3}} \right. \; \; \to \; \; x_1=1\; ,\; x_2=4$

$2)\; \; x^2=3-2x\\\\y=x^2\; ,\; y=3-2x\; \; \to \; \; x_1=-3\; ,\; x_2=1$

$3)\; \; x(a^2+3)=9x-a\\\\x=1:\; a^2+3=9-a\; \; ,\; \; a^2+a-6=0\; ,\; \; a_1=-3\; ,\; x_2=2\\\\Proverka:\; \; a_1=-3:\; \; x\cdot 12=9x+3\; ,\; \; 3x=3\; ,\; \; x=1\\\\a_2=2:\; \; x\cdot 7=9x-2\; ,\; \; 2x=2\; ,\; x=1\\\\Otvet:\; \; a_1=-3\; ,\; a_2=2\; .$

Answer 2

Задание 1

a)

$2x^2 - x = 0\\\\x(2x-1) = 0\\\\x_1 = 0\\\\2x - 1 = 0\\\\2x = 1\\\\x_2 = \frac{1}{2}$

б)

$9 - x^2 = 0\\\\-x^2 = -9\\\\x^2 = 9\\\\x_1 = 3\\\\x_2 = -3$

в)

$2x^2 - x - 1 = 0\\\\D = 1 + 8 = 9\\\\\sqrt{D} = 3\\\\x_1 = \frac{1-3}{4} = -\frac{2}{4} = -\frac{1}{2}\\\\x_2 = \frac{1+3}{4} = \frac{4}{4} = 1$

г)

$\frac{x^2}{x+6} = 1\\\\x\neq-6\\\\x^2 = x+6\\\\x^2 - x - 6 = 0\\\\D = 1 + 24 = 25\\\\\sqrt{D} = 5\\\\x_1 = \frac{1-5}{2} = \frac{-4}{2} = -2\\\\x_2 = \frac{1+5}{2} = \frac{6}{2} = 3$

д)

$\frac{x^2+2x}{x-1} = \frac{3}{x-1}\\\\x\neq1\\\\x^2+2x=3\\\\x^2 +2x - 3 = 0\\\\D = 4 + 12 = 16\\\\\sqrt{D} = 4\\\\x_1 = \frac{-2-4}{2} = -\frac{6}{2} = -3\\\\x_2 = \frac{-2+4}{2} =\frac{2}{2} = 1$

Как мы видим ОДЗ запрещает корень $x_2$. Поэтому решением данного уравнения будет только корень $x_1 = -3$.

е)

$\frac{5}{x+1} + \frac{4}{x-2} = \frac{3}{x-3}\\\\x\neq-1; x\neq2; x\neq3\\\\5(x-2)(x-3) + 4(x+1)(x-3) = 3(x+1)(x-2)\\\\5(x^2-3x-2x+6) + 4(x^2-3x+x-3) - 3(x^2-2x+x-2) = 0\\\\5(x^2-5x+6) + 4(x^2-2x-3) - 3(x^2-x-2) = 0\\\\5x^2 - 25x + 30 + 4x^2 - 8x - 12 - 3x^2+ 3x + 6 = 0\\\\6x^2 - 30x +24 = 0 |:6\\\\x^2 - 5x + 4 = 0\\\\D = 25 - 16 = 9\\\\\sqrt{D} = 3\\\\x_1 = \frac{5-3}{2} = \frac{2}{2} = 1\\\\x_2 = \frac{5+3}{2} = \frac{8}{2} = 4$

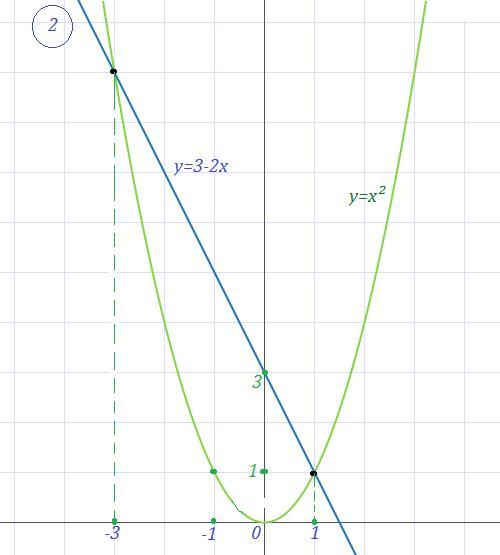
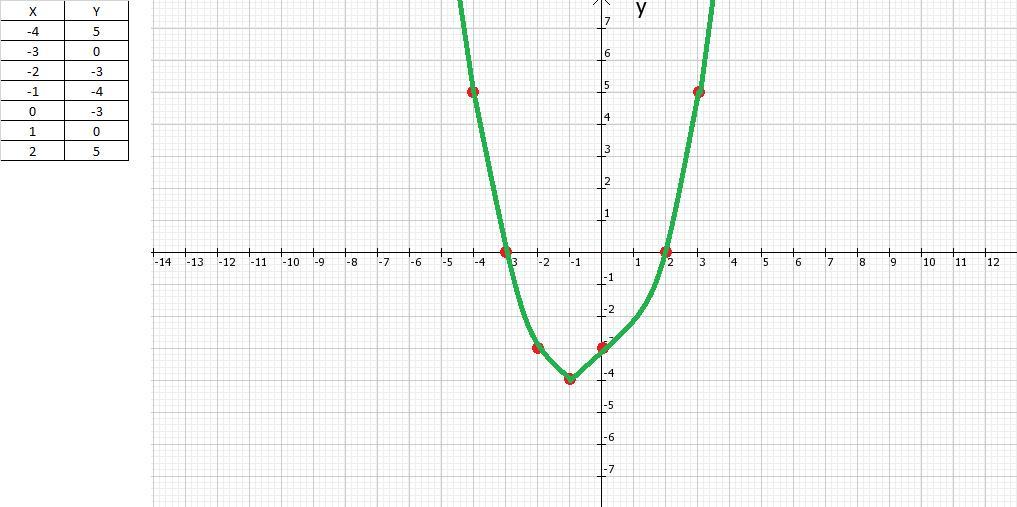
Задание 2.

$x^2 = 3-2x\\\\x^2 + 2x - 3 = 0\\\\D = 4 + 12 = 16\\\\\sqrt{D} = 4\\\\x_1 = \frac{-2-2}{2} = \frac{-4}{2} = -2\\\\x_2 = \frac{-2+2}{2} = \frac{0}{2} = 0$

Теперь найдём вершину параболы. По оси $x$ это будет $\frac{-b}{2a} = \frac{-2}{2} = -1$.

По оси $y$ это будет $-\frac{b^2-4ac}{4a} = -\frac{16}{4} = -4$.

Итак, координаты вершины параболы: $(-1; -4)$.

График в приложении.

Задание 3

Чтобы это выяснить, нужно подставить вместо $x$ значение 1

$a^2 + 3 = 9 - a\\\\a^2 + a + 3 - 9 = 0\\\\a^2 + a - 6 = 0\\\\D =1 + 24 = 25\\\\\sqrt{D} = 5\\\\a_1 = \frac{-1-5}{2} = -\frac{6}{2} = -3\\\\a_2 = \frac{-1+5}{2} = \frac{4}{2} = 2$

Итак, $x = 1$ при $a = -3$ и при $a = 2$.