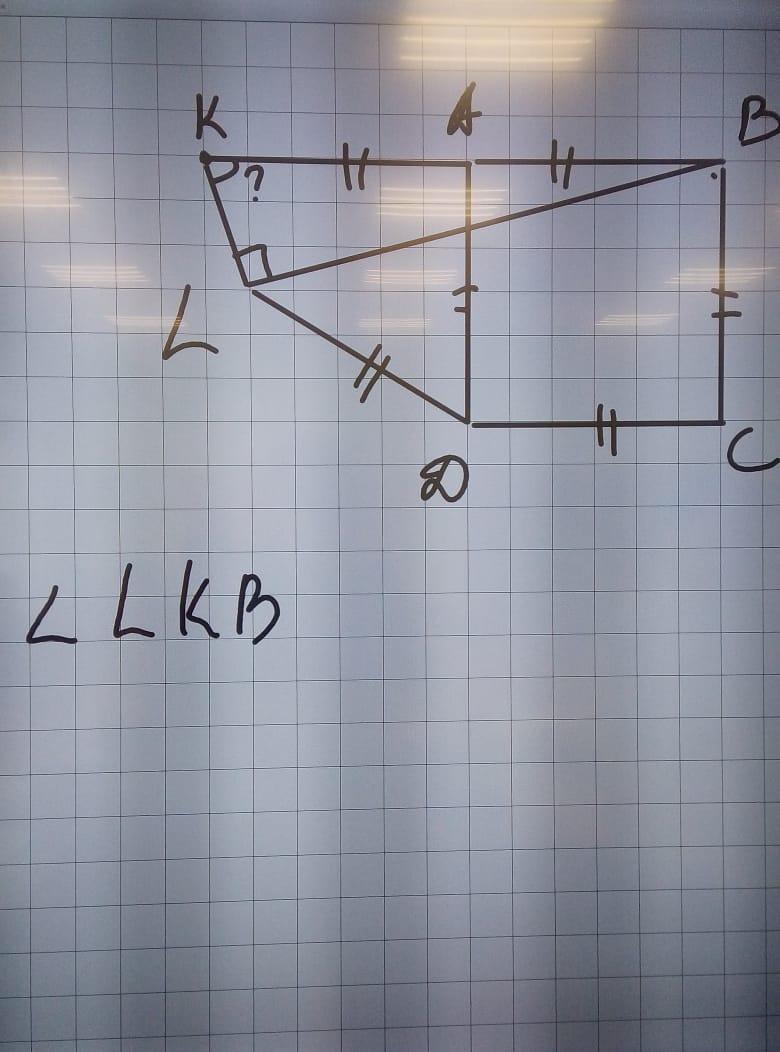
Помогите! Даю 50 баллов
Ответы
Відповідь:
Пояснення:

Ответ:
∠LКВ = 30° + α/2.
В частном случае, когда α = 90° (четырехугольник АВСD - квадрат), ∠LКВ = 30° + 45° = 75°.
Объяснение:
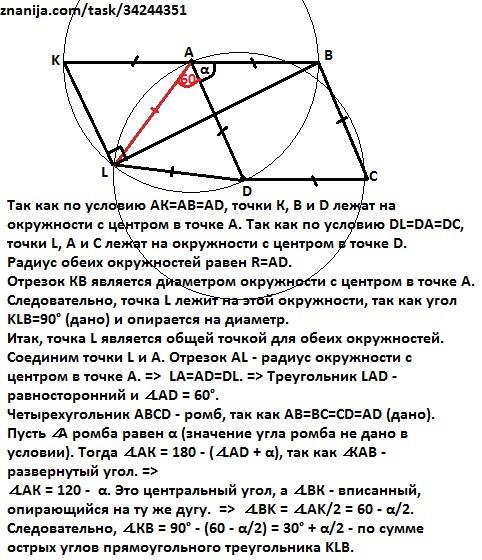
Так как по условию АК=АВ=AD, точки К, В и D лежат на окружности с центром в точке А.
Так как по условию DL=DА=DC, точки L, A и C лежат на окружности с центром в точке D.
Радиус обеих окружностей равен R=AD.
Отрезок КВ является диаметром окружности с центром в точке А.
Следовательно, точка L лежит на этой окружности, так как угол KLB=90° (дано) и опирается на диаметр.
Итак, точка L является общей точкой для обеих окружностей.
Соединим точки L и А. Отрезок AL - радиус окружности с центром в точке А. => LA=AD=DL. => Треугольник LAD - равносторонний и ∠LAD = 60°.
Четырехугольник АВСD - ромб, так как АВ=ВС=СD=AD (дано).
Пусть ∠А ромба равен α (значение угла ромба не дано в условии).
Тогда ∠LAК = 180 - (∠LAD + α), так как ∠КАВ - развернутый угол. => ∠LAК = 120 - α. Это центральный угол, а ∠LВК - вписанный, опирающийся на ту же дугу. =>
∠LBK = ∠LAK/2 = 60 - α/2.
Следовательно, ∠LКВ = 90° - (60 - α/2) = 30° + α/2 - по сумме острых углов прямоугольного треугольника KLB.
Ответ: ∠LКВ = 30° + α/2.
В частном случае, когда α = 90° (четырехугольник АВСD - квадрат),
∠LКВ = 30° + 45° = 75°.