Question

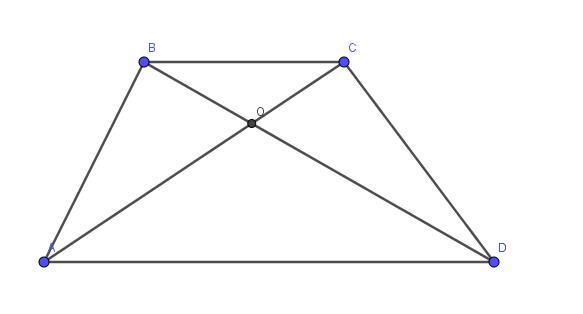
В трапеции АВСD с основаниями AD и BC диагонали пересекаются в точке О, BC:AD=3:5, BD=24см. Найдите отрезки BO, OD.

Answer 1

Рассмотрим треугольники AOD и BOC. $\angle AOD=\angle BOC$ как вертикальные. $\angle DAC=\angle ACB$ как накрест лежащие. Следовательно, треугольники AOD и BOC подобны (по двум углам). Из подобия треугольников следует пропорциональность соответствующих сторон

                         $\dfrac{BC}{AD}=\dfrac{BO}{OD}~~\Rightarrow~~~ \dfrac{BO}{OD}=\dfrac{3}{5}$

Пусть BO = 3x и OD = 5x, тогда BD = 8x , что по условию равен 24

8x = 24

x = 3

Следовательно, BO = 9 см и OD = 15 см