Предмет: Математика,
автор: kirillraut
Математики, влетайте =D
Вычислить предел, пользуясь правилом Лопиталя:
Приложения:
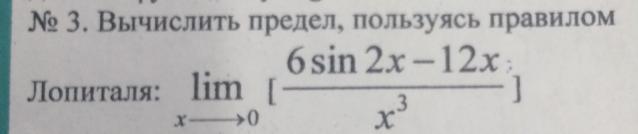
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: fascination
Предмет: Русский язык,
автор: Ленка29
Предмет: Математика,
автор: kotik3111
Предмет: Литература,
автор: ккк92