Предмет: Математика,
автор: ASV260
помогите решить 20 баллов
Приложения:
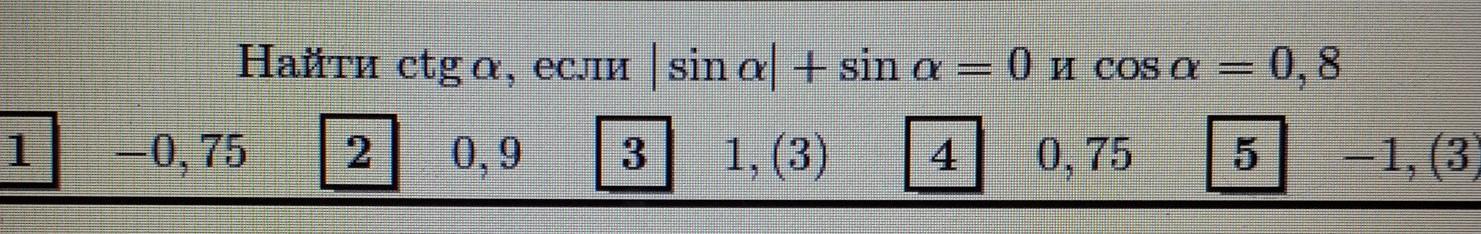
ASV260:
ну давайте
если |sina|+sina=0,при этом cos a=0.8-в какой четверти может находиться угол а?
|sina|=-sin a-значит sina отрицателен или 0
если честно, я не знаю
жаль
во второй, значит ctga отрицателен
есть формулы приведения
1+1/ctg^2 a=1/cos^2a
1/ctg^2 a=1/0.64-1
ctg^2a=0.64/0.36; ctg a=-8/6=-4/3=-1,(3)
Ответы
Автор ответа:
0
Так как cosα>0 , то угол α принадлежит 1 четверти или 4 четверти.
Из 1 условия следует, что .
По свойству модуля имеем : модуль какого-либо выражения равен противоположному выражению, если подмодульное выражение отрицательно. Следовательно, под знаком модуля функция . Тогда угол α принадлежит 3 четверти или 4 четверти.
Значит, из заданных условий делаем вывод, что угол α лежит в 4 четверти, а тогда сtgα<0 в 4 четверти.
Похожие вопросы
Предмет: Українська література,
автор: fgdsfhkg
Предмет: Русский язык,
автор: ZINAIDA
Предмет: Английский язык,
автор: dea
Предмет: Литература,
автор: rahmatyllink
Предмет: Алгебра,
автор: nastusha2014879