Предмет: Алгебра,
автор: sinuginadara3
СРОЧНО! 50 БАЛЛОВ! Помогите решить 5 и 6 номер, пожалуйста!
Приложения:
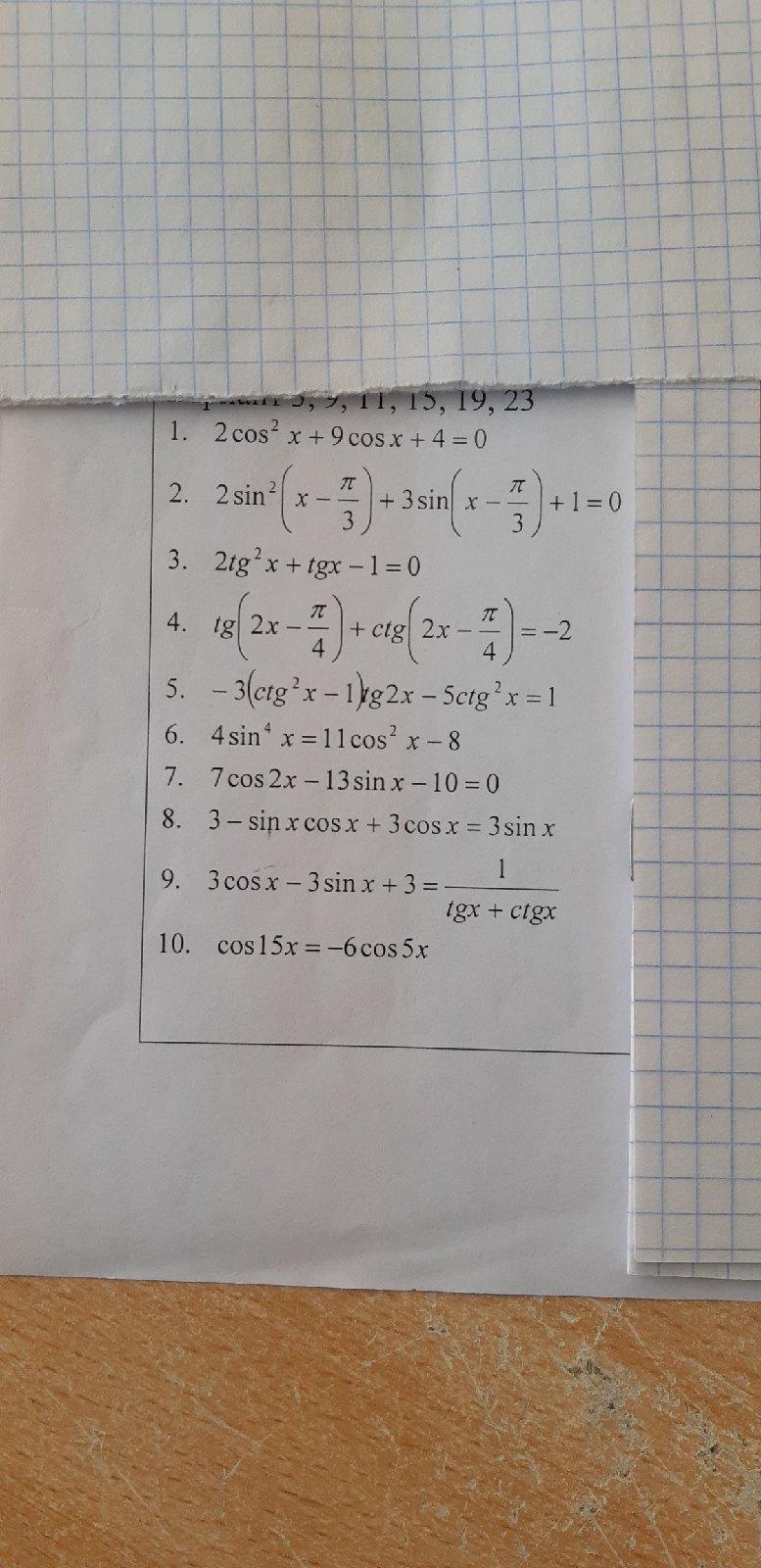
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Українська мова,
автор: lenavolk5
Предмет: Русский язык,
автор: Cesar
Предмет: Другие предметы,
автор: VladkaSolovuk
Предмет: Математика,
автор: LeraVolodko