В треугольнике сумма квадратов двух сторон в пять раз больше квадрата третьей
стороны. Определите величину наибольшего из углов, полученных при пересечении медиан
данного треугольника.
Ответы
Ответ:
Наибольший угол из углов, полученных при пересечении медиан данного треугольника равен 90°.
Объяснение:
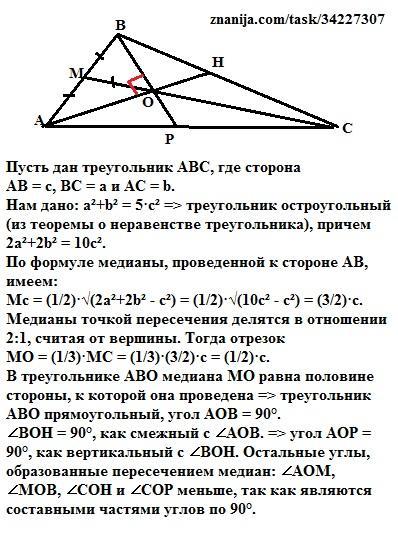
Пусть дан треугольник АВС, где сторона АВ = с, ВС = а и АС = b.
Нам дано: a²+b² = 5·c² => треугольник остроугольный (из теоремы о неравенстве треугольника), причем 2a²+2b² = 10c².
По формуле медианы, проведенной к стороне АВ, имеем:
Mc = (1/2)·√(2a²+2b² - c²) = (1/2)·√(10с² - c²) = (3/2)·с.
Медианы точкой пересечения делятся в отношении 2:1, считая от вершины. Тогда отрезок МО = (1/3)·МС = (1/3)·(3/2)·с = (1/2)·с.
В треугольнике АВО медиана МО равна половине стороны, к которой она проведена => треугольник АВО прямоугольный, угол АОВ = 90°.
∠ВОН = 90°, как смежный с ∠АОВ. => угол АОР = 90°, как вертикальный с ∠ВОН. Остальные углы, образованные пересечением медиан: ∠АОМ, ∠МОВ, ∠СОН и ∠СОР меньше, так как являются составными частями углов по 90°.