Question

Постройте график функции $y=\frac{{x}^{3}-2{x}^{2}-23x+60}{x-3}$ и определите при каком «k» прямая $y=kx-5$ имеет с графиком ровно одну общую точку

Answer 1

Область определения функции: $x-3\ne 0;~ x\ne 3$

$D(y)=(-\infty;3)\cup(3;+\infty)$

$y=\dfrac{x^3-2x^2-23x+60}{x-3}=\dfrac{x^3-3x^2+x^2-3x-20x+60}{x-3}=\\ \\ \\ =\dfrac{x^2(x-3)+x(x-3)-20(x-3)}{x-3}=x^2+x-20$

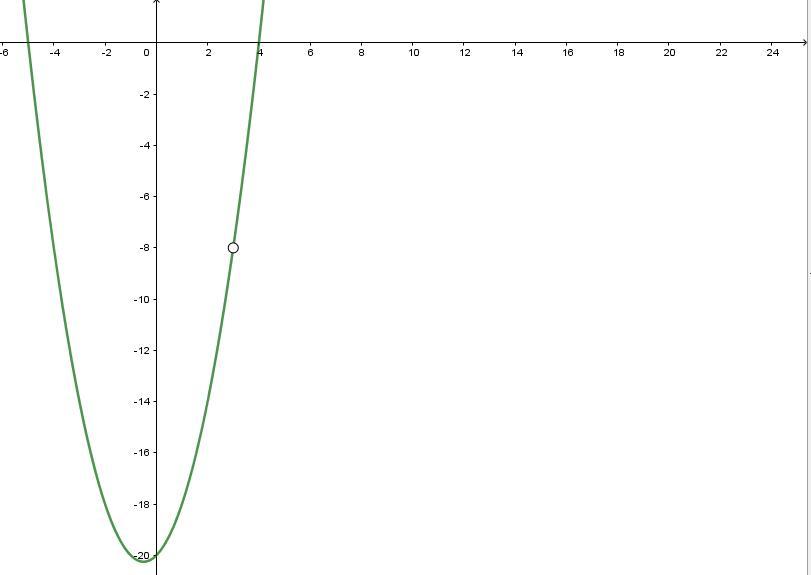
Это квадратичная функция, ее графиком является парабола, ветви которой направлены вверх.

$m=-\dfrac{b}{2a}=-\dfrac{1}{2}\\ \\ y=\dfrac{1}{4}-\dfrac{1}{2}-20=-20{,}25$

(-0,5; -20,25) - координаты вершины параболы.

Подставим y = kx - 5 в упрощенный график уравнения

$x^2+(1-k)x-15=0\\ D=(1-k)^2+60>0$

То есть, дискриминант положителен для всех k, т.е. уравнение имеет два корня.

График функции c прямой имеет ровно одну общую точку, когда эта прямая проходит через выколотую точку (3;-8)

-8 = 3k - 5

-3 = 3k

k = -1