Предмет: Математика,
автор: катюша20000
Помогите найти предел, очень срочнооо
Приложения:
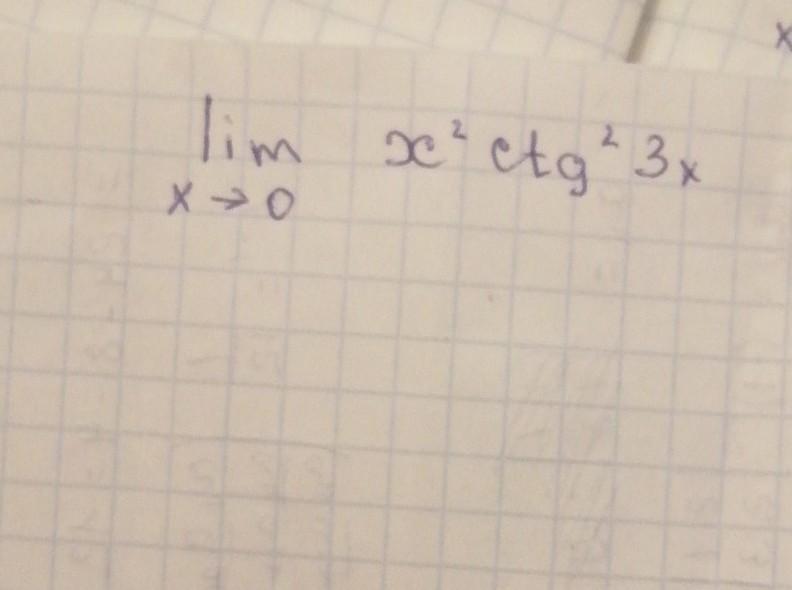
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
В последнем действии используем первый замечательный предел
Похожие вопросы
Предмет: Українська мова,
автор: cd95
Предмет: Русский язык,
автор: almaz2512
Предмет: Українська література,
автор: Юляша10299
Предмет: Математика,
автор: miaa