Решите пожалуйста с подробным объяснением
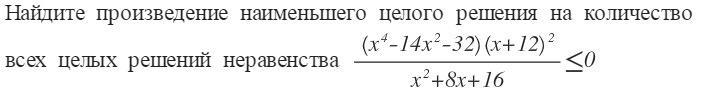
Ответы
Ответ: 8
Пошаговое объяснение:

Ответ:
-108
Пошаговое объяснение:
((x^4 -14x^2 -32)(x+12)^2)/(x^2 +8x+16)≤0
x^2 +8x+16≠0
Допустим:
x^2 +8x+16=0; D=64-64=0
x1=-8/2=-4
Следовательно, x1≠-4.
x^4 -14x^2 -32≤0
Допустим:
x^4 -14x^2 -32=0; x^2=t
t^2 -14t-32=0
t1+t2=14; 16-2=14
t1•t2=-32; 16•(-2)=-32
t1=16; x^2=16; x2=-4 - но x1≠-4.
При x2<-4:
-5^4 -14•(-5)^2 -32≤0
625-350-32≤0
243>0
Следовательно, неравенство не соблюдается.
При x2>-4:
0^4 -14•0^2 -32≤0
-32<0
Следовательно, x2>-4.
x^2=16; x3=4
При x3<4:
0^4 -14•0^2 -32≤0
-32<0
Следовательно, x3<4.
При x3=4:
256-14•16-32≤0
256-224-32≤0
0=0
Следовательно, x3=4, а значит x3≤4.
При x3>4:
5^4 -14•5^2 -32≤0
625-350-32≤0
243>0
Следовательно, неравенство не соблюдается.
t2=-2; x^2=-2 - этот корень не подходит.
(x+12)^2≤0
Допустим:
(x+12)^2=0
х+12=0
х4=-12
При x4>-12:
(-11+12)^2≤0
1>0
Следовательно, неравенство не соблюдается.
При x4<-12:
(--13+12)^2≤0
1>0
Следовательно, неравенство не соблюдается.
При x4=-12:
(-12+12)^2≤0
0=0
Следовательно, x4=-12.
Вывод: x принадлежит {-12} объединяет (-4; 4].
Наименьший корень: -12, всего целых корней: 9.
Ответ: -12•9=-108.