Предмет: Алгебра,
автор: TequilaSunrise
помогите, пожалуйста, максимально подробно нужно
Приложения:
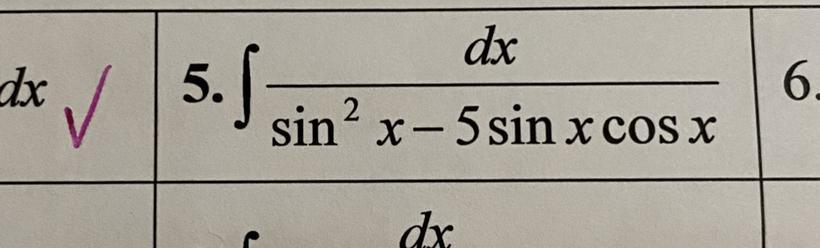
Ответы
Автор ответа:
2
1. Воспользуемся универсальной тригонометрической подстановкой:
2. Преобразовав интеграл, воспользуемся методом неопределённых коэффициентов:
3. Перейдём в систему уравнений:
Сумма A+B = 0, потому что окончательном варианте шага 1, мы не имеем в числителе слагаемых содержащих переменную t, но есть "невидимая" 1, на которую умножается dt.
4. Подставим в нач данные уже найденные коэффициенты в шаг 2:
4.1. Разбиваем неопределённый интеграл на 2 части, при этом вынося коэффициент, стоящий в числителе:
5. Выполняю обратную подстановку:
Похожие вопросы
Предмет: Українська література,
автор: cd95
Предмет: Українська література,
автор: ДОПОМОЖІТЬ
Предмет: Українська література,
автор: Snizhana
Предмет: Математика,
автор: Глеб010205
Предмет: Математика,
автор: danialblacva