Предмет: Математика,
автор: Kate7219999999
Помогите, пожалуйста решить задание
по математической статистики
Приложения:
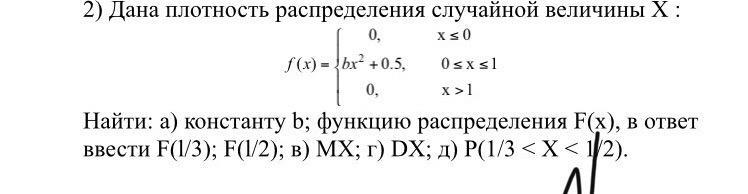
Ответы
Автор ответа:
1
а) Поиск константы b
б) Поиск функции распределения F(x) и F(1/3), F(1/2)
Итого:
Найдём F(1/3) и F(1/2):
в) Поиск математического ожидания
г) Поиск дисперсии
д) Поиск P(1/3 < X < 1/2)
Похожие вопросы
Предмет: Русский язык,
автор: elena22031976
Предмет: Українська мова,
автор: Naruto1
Предмет: Русский язык,
автор: семишкин
Предмет: Математика,
автор: богдан27062005