Question

Срочно
Ребят
Геометрия
Пожаалуйста

Answer 1

Ответ:

(АВ^AC) = α = arccos0,786 ≈ 38°

Объяснение:

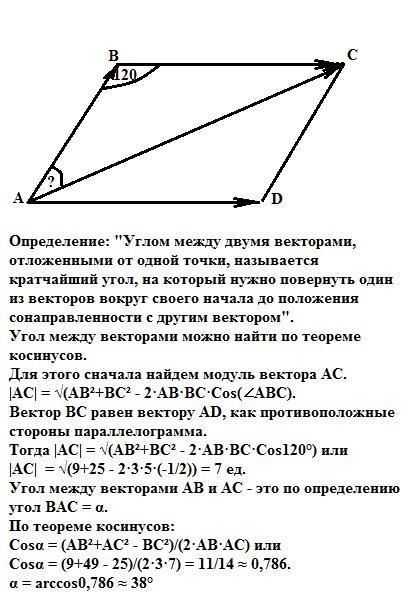
Определение: "Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором".

Угол между векторами можно найти по теореме косинусов.

Для этого сначала найдем модуль вектора АС.

|AC| = √(АВ²+ВС² - 2·AB·ВС·Cos(∠АВС).

Вектор ВС равен вектору AD, как противоположные стороны параллелограмма.

Тогда |AC| = √(АВ²+ВС² - 2·AB·ВС·Cos120°) или

|AC| =  √(9+25 - 2·3·5·(-1/2)) = 7 ед.

Угол между векторами АВ и AС - это по определению

угол ВАС = α.

По теореме косинусов:

Cosα = (AB²+AС² - BC²)/(2·AB·AС) или

Cosα = (9+49 - 25)/(2·3·7) = 11/14 ≈ 0,786.

α = arccos0,786 ≈ 38°