Question

ДАЮ 100 БАЛЛОВ!!!

Стороны прямоугольника меньше его диагонали на 4см и8см соответственно.
а)Найти площадь прямоугольника.
б) Найти площадь квадрата, периметр которого равен периметру прямоугольника.

Answer 1

Ответ:

192 см²;  196 cм²

Объяснение:

Дано: СКМТ - прямоугольник, СМ - диагональ, СТ=СМ-4 см;  МТ=СМ-8 см. Найти S; Р; Sквадрата.

Рассмотрим ΔСМТ - прямоугольный.

Пусть СМ=х см, тогда СТ=х-4 см;  МТ=х-8 см.

По теореме Пифагора

х²=(х-4)²+(х-8)²

х²=х²-8х+16+х²-16х+64

х²-24х+80=0

По теореме Виета х=4 (не подходит по условию)  и х=20.

СМ=20 см,  СТ=20-4=16 см;  МТ=20-8=12 см

S(CКМТ)=СТ*МТ=16*12=192 см²

Р(СКМТ)=2(16+12)=56 см

Рквадрата=56 см;  сторона квадрата а=56:4=14 см;  площадь квадрата S=14²=196 cм²

Answer 2

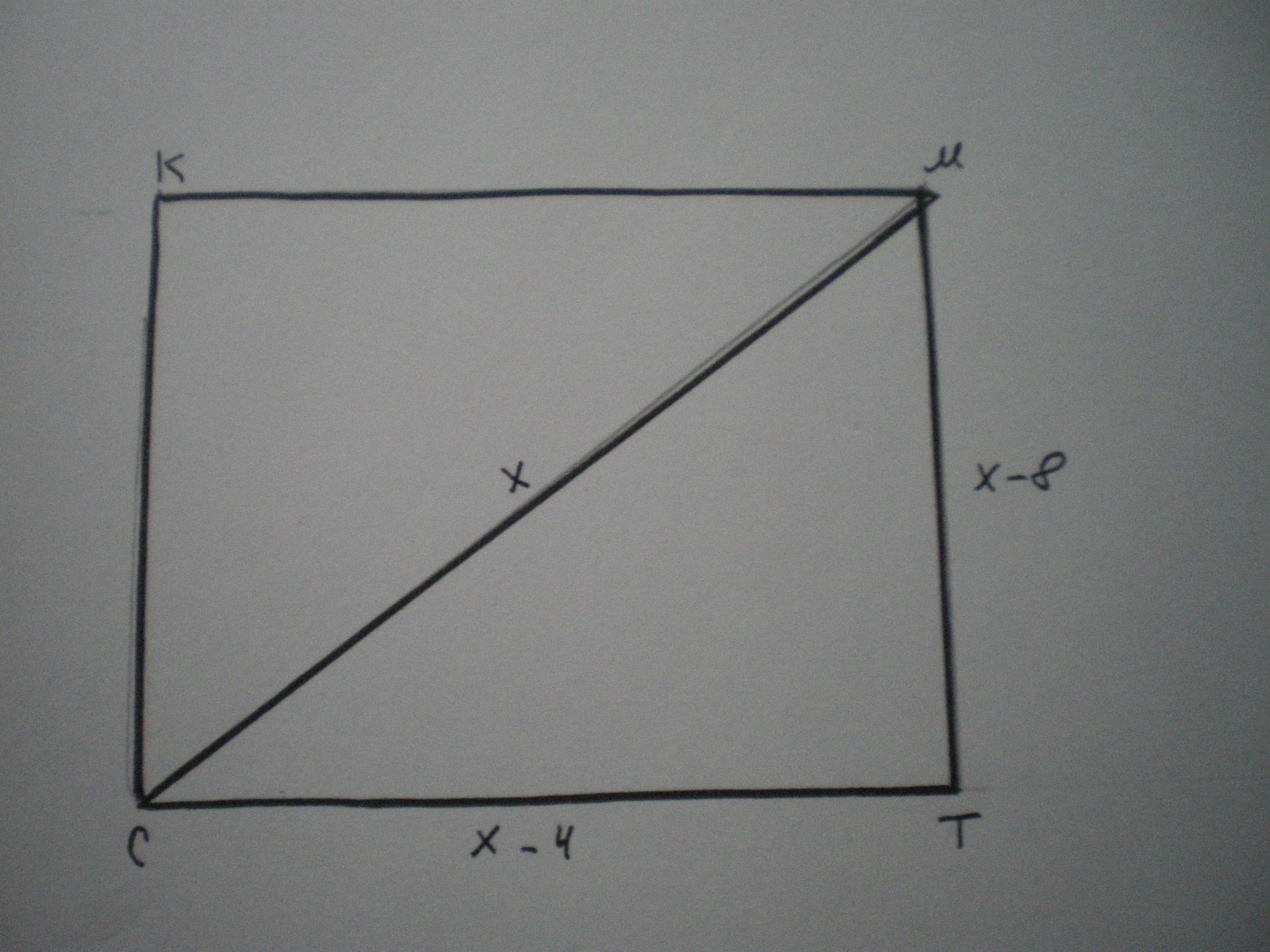
Если диагональ х см, то стороны соответственно (х-4) см и (х-8) см.

Т.к. диагональ делит прямоугольник на два равных прямоугольных треугольника, то квадрат диагонали прямоугольника равен сумме квадратов его сторон, по  Пифагору.

(х-4)²+(х-8)²=х²;      х²-8х+16+х²-16х+64=х²;  х²-24х+80=0; х=12±√(144-80)=

12±8; Значит,  диагональ или 20см или 4см, но она должна быть больше сторон, а у нас получилась равна стороне, поэтому х=4 не подходит по смыслу задачи. Если диагональ 20 см, то одна сторона  20-4=16 (см), а другая 20-8=12 (см).

Площадь прямоугольника равна 16*12=192(см²), Периметр прямоугольника равен (16+12)*2=56 (см), если он равен периметру квадрата, то сторона квадрата равна 56/4=14(см), тогда площадь такого квадрата равна 14²=196(см²)