Предмет: Математика,
автор: PARARALON
Найти производную функции y=cos3x / 1-sin3x
Приложения:
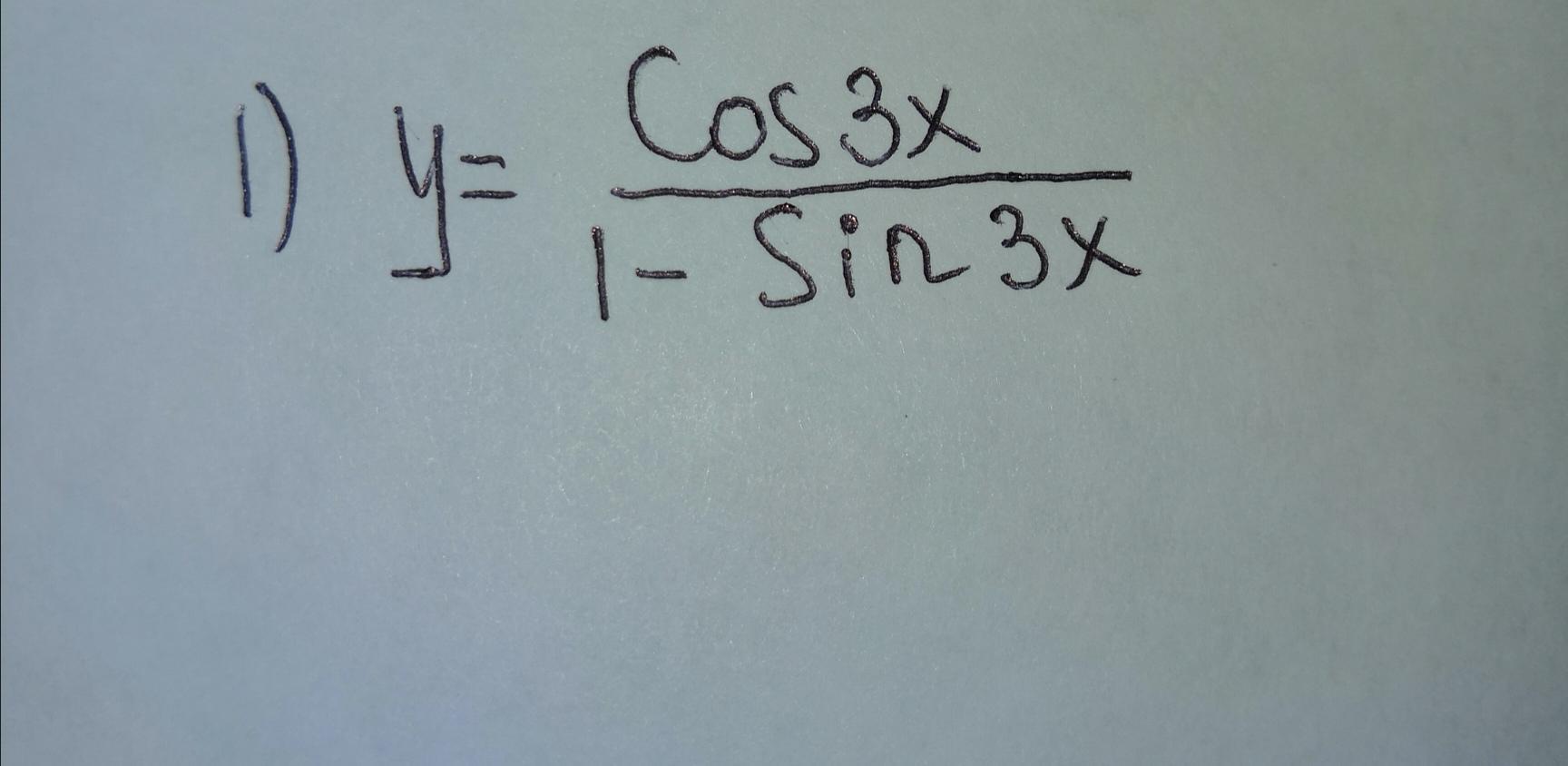
Ответы
Автор ответа:
1
PARARALON:
Надо ли в данном примере сначала раскрыть сложную функцию Cos3x?
естественно надо учесть ,что cos3x - сложная функция, это и сделано при нахождении её производной
см. добавила...
Автор ответа:
0
Ответ: во вложении Пошаговое объяснение:
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: нусик
Предмет: Русский язык,
автор: АЛИНУСИК1
Предмет: Русский язык,
автор: heccrbq
Предмет: Физика,
автор: 228753