Предмет: Алгебра,
автор: tkaa
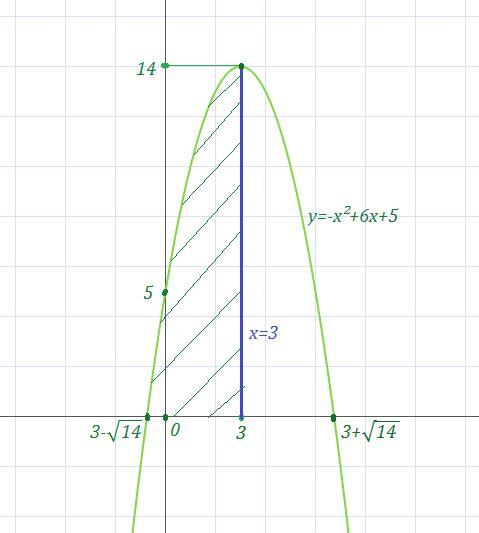
Помогите пож СРОЧНО! Вычислите площадь фигуры, ограниченной линиями y=-x^2+6x+5; y=0; x=3
Ответы
Автор ответа:
0
Приложения:
Похожие вопросы
Предмет: Математика,
автор: anonimusuuu
Предмет: Математика,
автор: dasagerasimcuk2
Предмет: Українська мова,
автор: Аноним
Предмет: Биология,
автор: dasha16horse