Question

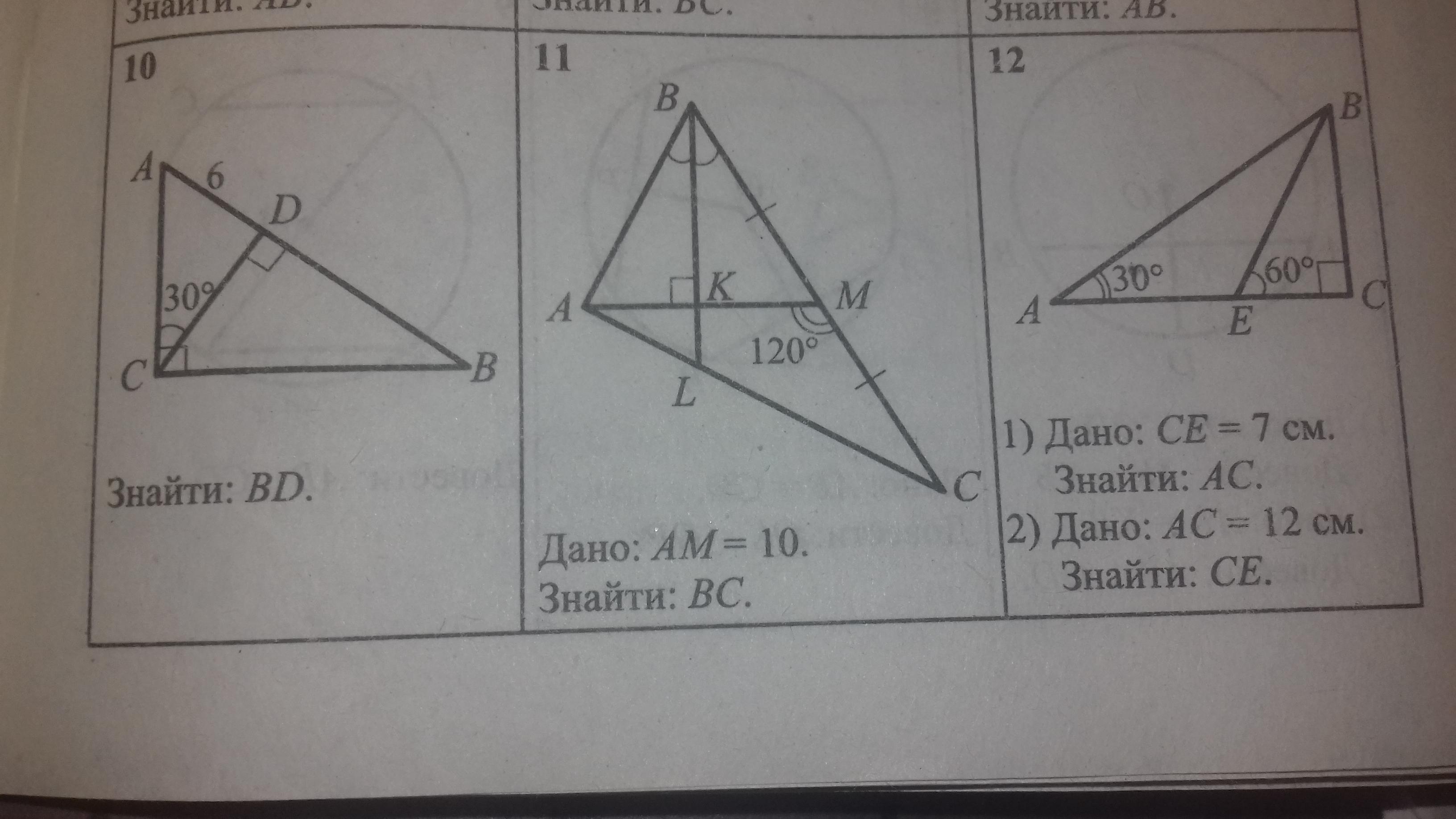
Решите пожалуйста таблица 7.15 10, 11 и 12. ДАЮ 50 БАЛЛОВ

Answer 1

(*) В прямоугольном треугольнике напротив угла в 30° лежит катет в два раза меньше гипотенузы. Теорема будет часто применяться.

10. Из ΔADC по теор. (*) 2AD = AC ⇒ AC = 12

По теореме Пифагора в ΔADC:

$CD=\sqrt{AC^2-AD^2}=\sqrt{12^2-6^2}=\sqrt{108}=6\sqrt{3}$

∠DCB = ∠ACB - ∠ACD = 90° - 30° = 60°

∠DBC = 180° - ∠CDB - ∠DCB = 30° (теор. о сумме углов Δ)

В ΔCBD по теор. (*) 2CD = CB ⇒ CB = 12√3

По теореме Пифагора в ΔBDC:

$BD=\sqrt{BC^2-CD^2}=\sqrt{144\cdot 3-36\cdot3}=\sqrt{324}=18$

Ответ: 18

11. ∠BMA = 180° - ∠AMC = 180° - 120° = 60° (смежные углы)

∠MBK = 180° - ∠BKM - ∠BMK = 30° (теор. о сумме углов Δ)

∠MBK = ∠ABK (по условию) ⇒ ∠ABM = 60°

∠ABM = ∠BMA = 60° ⇒ ΔABM -- равносторонний ⇒ AM = BM = 10

BC = BM + MC = 2BM = 20

Ответ: 20

12. 1) ∠EBC = 180° - ∠BEC - ∠ECB = 30° (теор. о сумме углов Δ)

Из ΔBEC по теор. (*) 2EC = CB ⇒ CB = 14 см

Из ΔABC по теор. (*) 2BC = AB ⇒ AB = 28 см

По теореме Пифагора в ΔABC:

$AC=\sqrt{AB^2-BC^2}=\sqrt{28^2-14^2}=\sqrt{588}=14\sqrt{3}cm$

Ответ: 14√3 см

12. 2) Из ΔABC по теор. (*) 2BC = AB

Пусть BC = x см, тогда AB = 2x см. По теореме Пифагора составим уравнение:

$AB^2=BC^2+AC^2\\4x^2=x^2+144\\x^2=48\\x=4\sqrt{3} cm$

BC = 4√3 см

∠EBC = 180° - ∠BEC - ∠ECB = 30° (теор. о сумме углов Δ)

Из ΔBEC по теор. (*) 2EC = BC ⇒ EC = 2√3 см

Ответ: 2√3 см