По стороне основание а=4 и по апофеме d=6 найдите площадь полной поверхности правильной призмы а)треугольной , б)Четырехугольной , в) Шестиугольной .
Помогите пожалуйста
Ответы
Sполн. пов. = 2Sосн. + Sбок. пов.
Sбок. пов. можно искать как сумму площадей боковых граней.
Также Sбок. пов. = Pосн. * d, где d -- высота призмы, а Pосн. -- периметр основания призмы.
(чтобы получить такую формулу, нужно записать сумму площадей боковых граней и вынести за скобку высоту d)
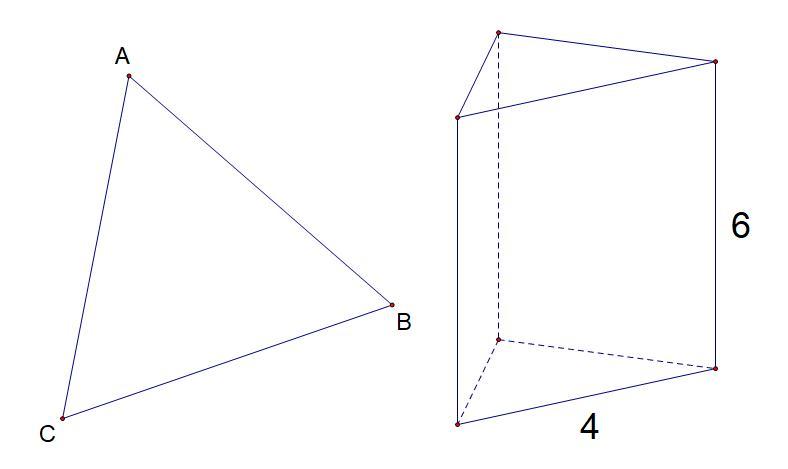
a) Треугольная правильная призма.
Sбок.пов. = PΔABC * d = 3a * d = 12 * 6 = 72
Sполн. пов. = 2Sосн. + Sбок.пов. = 2 * 4√3 + 72 = 8(9 + √3)
Ответ: 8(9 + √3)
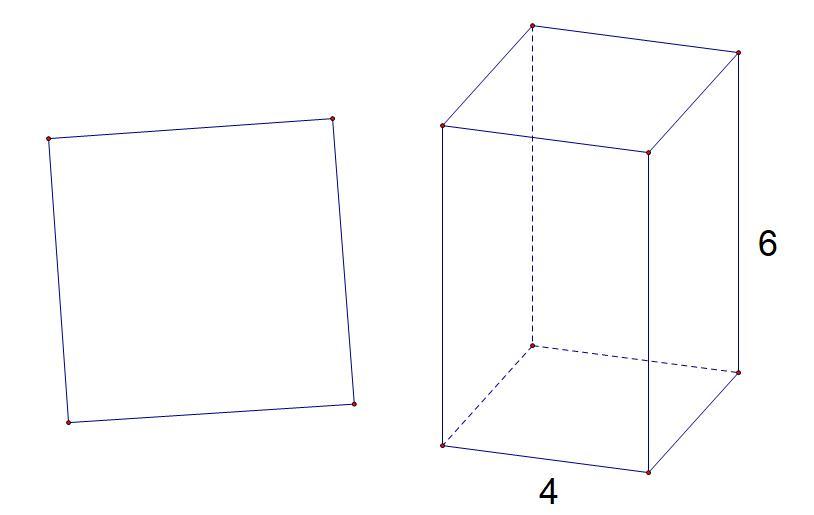
б) Четырёхугольная правильная призма.
Sбок.пов. = Pосн. * d = 4a * d = 16 * 6 = 96
Sосн. = a² = 16
Sполн. пов. = 2Sосн. + Sбок.пов. = 32 + 96 = 128
Ответ: 128
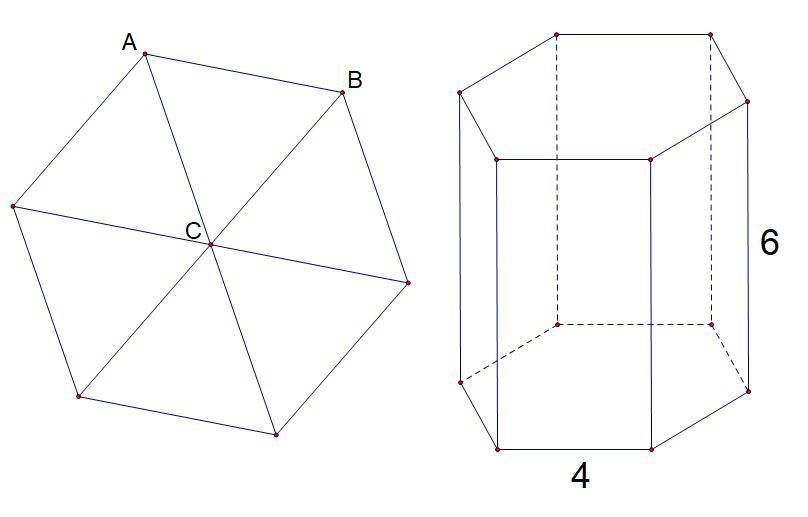
в) Шестиугольная правильная призма.
Sбок.пов. = Pосн. * d = 6a * d = 24 * 6 = 144
Sосн. = 6SΔABC
Заметим, что ΔABC такой же, как в задаче а), поэтому
Sосн. = 6SΔABC = 6 * 4√3 = 24√3
Sполн. пов. = 2Sосн. + Sбок.пов. = 48√3 + 144 = 48(3 + √3)
Ответ: 48(3 + √3)