Question

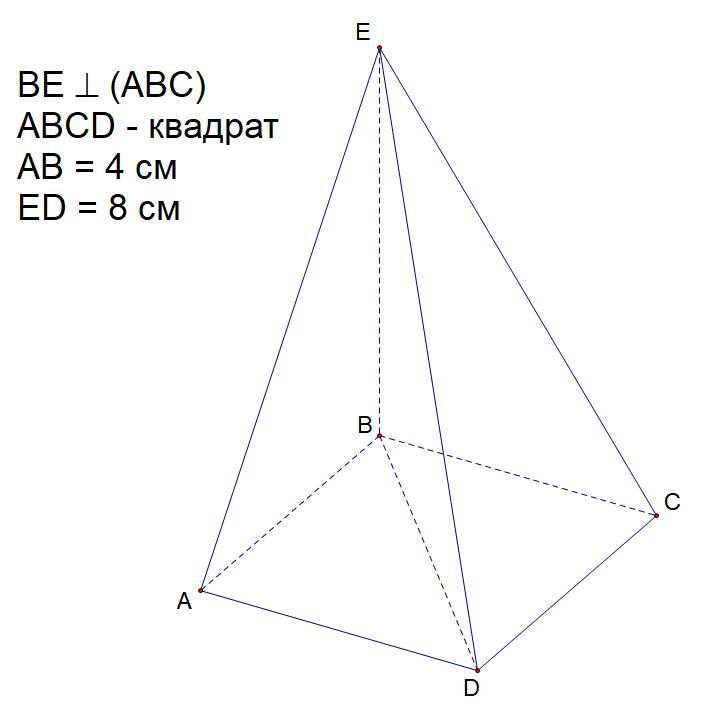
Основанием пирамиды является квадрат со стороной 4 см .Одно их боковых ребер перпендикулярно к плоскости основания .Наибольшее боковое ребро равно 8 см.Найдите высоту пирамиды.
Помогите пожалуйста

Answer 1

Ответ: 4√2 см

Объяснение:

В начале находится наибольшее боковое ребро, которое указано на картинке, как данное.

1. BE -- перпендикуляр к (ABC), а значит наименьшее боковое ребро.

Рассмотрим ΔAEB, ΔBEC и ΔBED

BE ⊥ (ABC) ⇒ BE ⊥ любой прямой в (ABC) ⇒ треугольники прямоугольные.

Тогда боковые ребра AE, ED и EC можно найти по теореме Пифагора.

Причём под корнем будет стоять сумма квадратов EB и другого катета (свой для каждого случая). Чем больше будет этот катет, тем больше боковое ребро. То есть надо сравнить стороны AB, BD, BC.

Из них диагональ квадрата -- наибольшая ⇒ ED -- наибольшее боковое ребро ⇒ ED = 8 см

2. Рассмотрим ΔABD:

∠A = 90° (квадрат), AB = AD = 4 см (условие)

По теореме Пифагора:

$BD=\sqrt{AB^2+AD^2}=\sqrt{4^2+4^2}=\sqrt{32}=4\sqrt{2}cm$

3. Рассмотрим ΔBDE:

∠B = 90° (BE ⊥ любой прямой в (ABC)), BD = 4√2 см (п. 2), ED = 8 см (п. 1)

По теореме Пифагора:

$BE=\sqrt{DE^2-BD^2}=\sqrt{8^2-(4\sqrt{2})^2}=\sqrt{64-32}=\sqrt{32} =4\sqrt{2}cm$