Предмет: Алгебра,
автор: Yenn45
Алгебра, 10 класс, логарифмическое неравенство
Приложения:
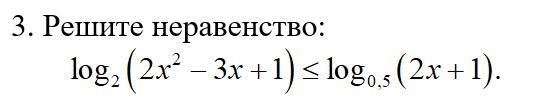
Ответы
Автор ответа:
1
ОДЗ :
1) 2x² - 3x + 1 >0
2(x - 1)(x - 0,5) > 0
(x - 1)(x - 0,5) > 0
+ - +
________₀_________₀_________
0,5 1
///////////////// ////////////////////
x ∈ (- ∞ ; 0,5) ∪ (1 ; +∞)
2) 2x + 1 > 0
2x > - 1
x > - 0,5
Окончательно : x ∈ (- 0,5 ; 0,5) ∪ (1 ; + ∞)
Похожие вопросы
Предмет: Алгебра,
автор: dmitroderebcinskij
Предмет: Русский язык,
автор: stepaloxgxgsg
Предмет: Русский язык,
автор: gorbunovaviktoria198
Предмет: Геометрия,
автор: Аншлак
Предмет: История,
автор: swastiji140