Предмет: Алгебра,
автор: Аноним
Решите уравнение.
Мне нужно решить (а).
Приложения:
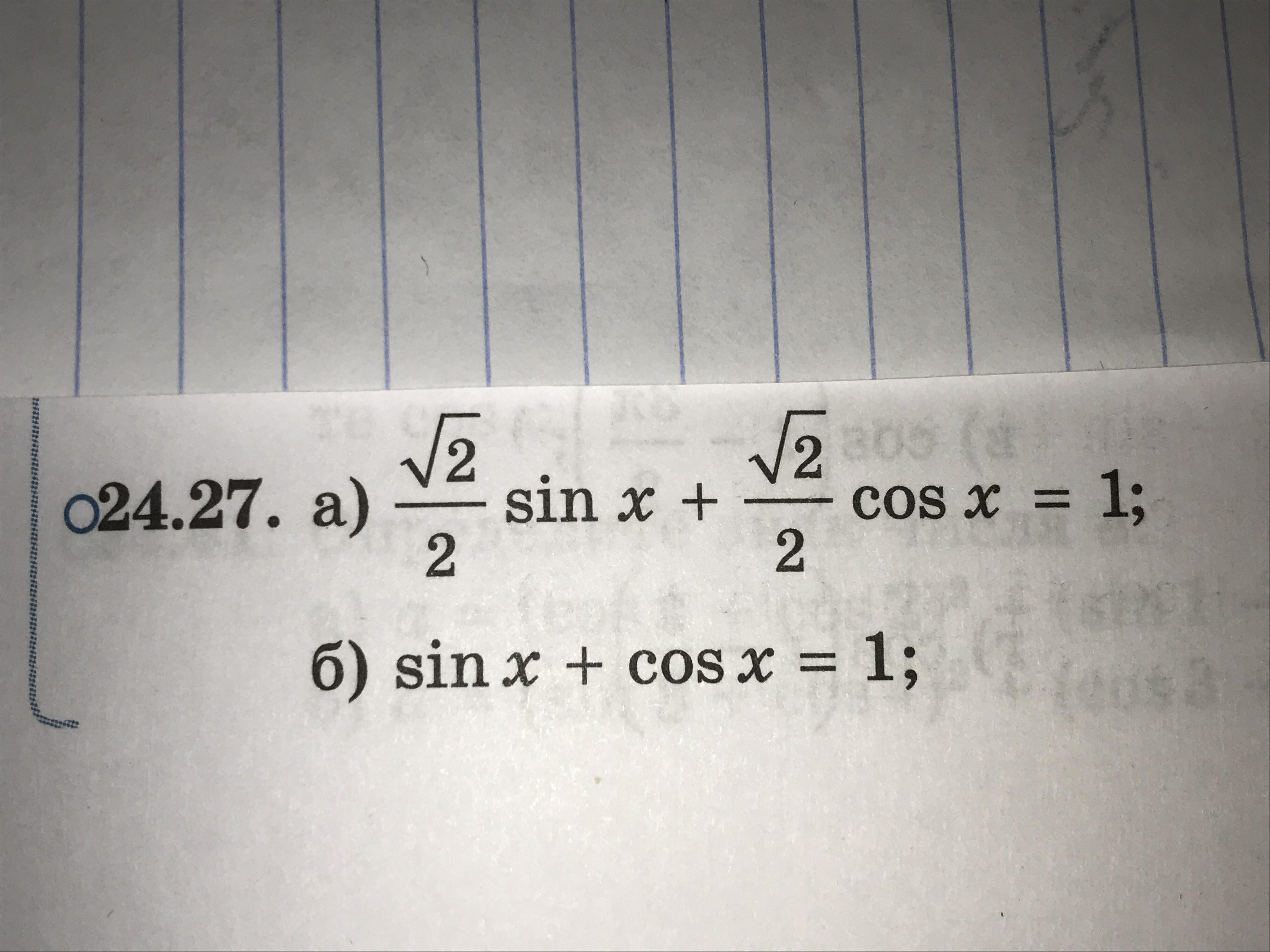
Ответы
Автор ответа:
0
Объяснение:
а)
преобразуем
возведем в квадрат левую и правую часть с учётом sin(x)+cos(x)>0
так как при n=2k+1, sin(x)+cos(x)<0, то получаем
б) аналогично примеру а) возводим в квадрат правую и левую части и получаем
так как при n=4k+2 и n=4k+3 получаем отрицательные значения sin(x)+cos(x), а точнее равное -1
то решение можно представить в виде:
Аноним:
результат верный, но зачем так сложно. Смотри решение IgorShap. Второе уравнение решается аналогично после умножения на sqrt(2)/2
кому как больше нравится, сложность вижу только в одном - исключение значений sinx+cosx<0, а так не вижу никакой сложности
Автор ответа:
0
sin(α+β) = sin(α)·cos(β) + cos(α)·sin(β)
Похожие вопросы
Предмет: Биология,
автор: vvensisv
Предмет: Алгебра,
автор: mseva6454
Предмет: Английский язык,
автор: lukasylenko
Предмет: Обществознание,
автор: Egor9klass
Предмет: Математика,
автор: alekseevaa3