Предмет: Алгебра,
автор: dima56764
ПОМОГИТЕ ПОЖАЛУЙСТА ДАЮ 30
Приложения:

Ответы
Автор ответа:
0
Приложения:
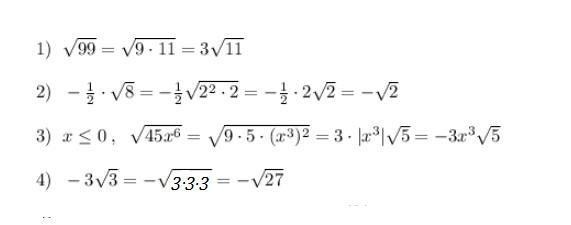
Похожие вопросы
Предмет: Русский язык,
автор: botagozkujlukova
Предмет: Алгебра,
автор: dasagrigorenko02
Предмет: Алгебра,
автор: negrq23231
Предмет: Математика,
автор: yulechkabelova
Предмет: Математика,
автор: Safina2005