Предмет: Алгебра,
автор: LSM54
(x-1)^2(x-5)<0 Подробно решите неравенство
nikebod313:
Понятно решение?
Пожалуйста!
Ответы
Автор ответа:
1
Первый способ
Анализируем: здесь — неотрицательная величина; имеем: при умножении неотрицательной величины с другим выражением мы можем получить отрицательное число, если второе выражение будет отрицательным, а первое — не равным нулю:
Итак, общим ответом будет
Второй способ
Решим неравенство методом интервалов:
1) Найдем нули данного выражения:
2) ОДЗ: все числа
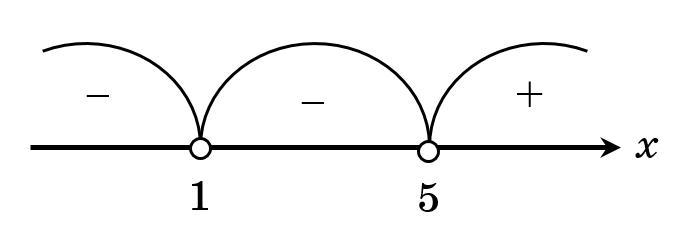
3) Начертим координатную прямую и отметим нули данного выражения выколотыми точками (так как неравенство строгое) и определим знак на каждом участке и объединим участок (участки), содержащие знак "минус" (см. вложение).
Итак, общим ответом будет
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: abdullaevaselima75
Предмет: Қазақ тiлi,
автор: amaniabdikarim
Предмет: Геометрия,
автор: jovohirsotiv64
Предмет: Математика,
автор: СайфЭмиль
Предмет: Биология,
автор: обезьяна55555