1.В прямой треугольной призме ребра основания равны 9см,10см,7см, а длина бокового ребра равна 15 см. Найдите площадь полной поверхности данной призмы.
2. См на картинке
3. См на картинке

Ответы
№ 1
1.В прямой треугольной призме ребра основания равны 9см, 10см ,7см, а длина бокового ребра равна 15 см. Найдите площадь полной поверхности данной призмы.
Решение:
Назовем нашу призму АВСА1В1С1.
S(п.п) = Sбок + 2Sосн
По бокам у нас 3 разных квадрата. Найдем Sбок:
Sбок = 9 * 15 + 7 * 15 + 10 * 15 = 390 см^2
В основании лежит прямоугольный треугольник. Площадь прямоугольного треугольника определяется по формуле:
S = 1/2 ab
S = 0.5 * 7 * 9 = 31.5 см^2
Тогда:
S(п.п) = 390 + 2 * 31,5 = 453 см^2
Ответ: 453 см^2
№ 2
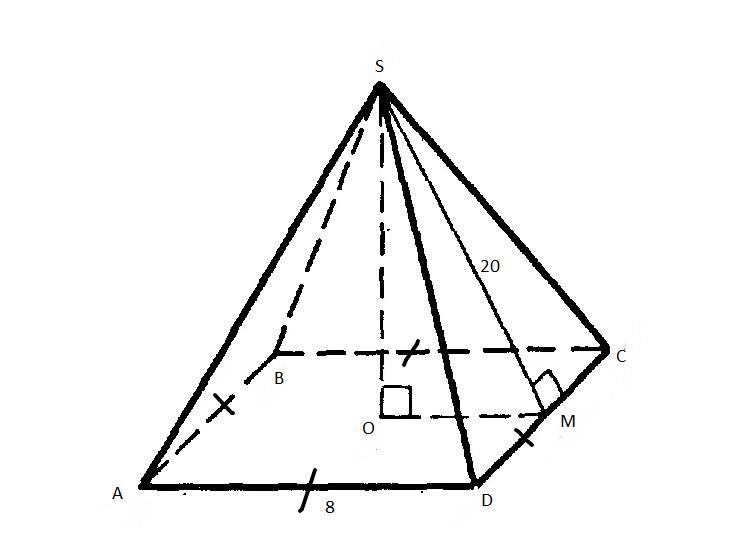
В правильной четырехугольной пирамиде ребро основания равно 8 м, боковое ребро равно 20 м. Найдите площадь полной поверхности пирамиды.
Решение:
S(п.п) = Sбок + Sосн
Sбок = 1/2 * 4а * h = 2ah
Sосн = a^2
S(п.п) = a^2 + 2ah = 8^2 + 2 * 8 * 20 = 64 + 320 = 384 см^2
Ответ: 384 см^2
№ 3
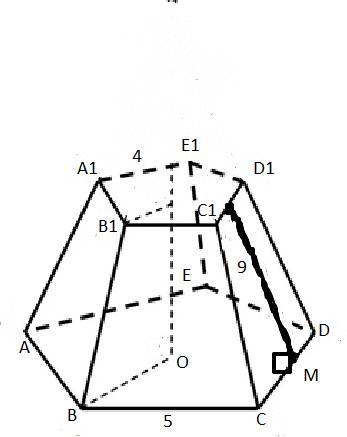
В правильной усеченной пятиугольной пирамиде апофема равна 9 дм, ребро верхнего основания равно 4 дм, ребро нижнего основания равно 5 дм. Найдите площадь боковой поверхности усеченной пирамиды.
Решение:
Все нашу боковую площадь составляют 5 одинаковых трапеций. Т.е, нам достаточно найти площадь трапеции.
Sтрап. = ½h(a+b)
Sтрап. = ½9(4+5) = 40,5 дм^2
Тогда:
Sбок = 40,5 * 5 = 202,5 дм^2
Ответ: 202,5 дм^2