Предмет: Математика,
автор: kseniyparsina
помогите пожалуйста решить 3 и 14 задание
Приложения:

Ответы
Автор ответа:
1
Ответ:
Найдем точки пересечения параболы y = x² - x и прямой y = 3x
Парабола и прямая пересекаются в точках (0; 0) и (4; 12)
Для того, чтобы получить площадь фигуры ограниченной линиями, необходимо вычислить определенный интеграл вида:
где a = x₁, b = x₂
Решение первого и второго см. на рисунке.
Приложения:
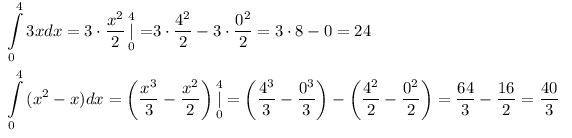
engineer54:
Это под номером 3)
спасибо)
Сейчас 14 гляну
Похожие вопросы
Предмет: Математика,
автор: suhrabisrailov7
Предмет: Қазақ тiлi,
автор: anton1990karbovski19
Предмет: Математика,
автор: galymbetovkozomberdi
Предмет: География,
автор: itnetcoll
Предмет: Физика,
автор: Kazakova822