Question

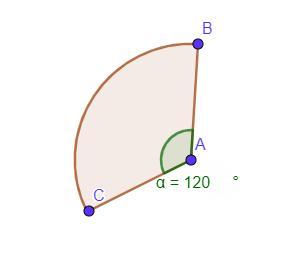
периметр осевого сечения конуса равен 24 см, угол развертки его боковой поверхности 120градусов. Вычислите площадь полной поверхности конуса

Answer 1

Ответ: 36п

Объяснение:

∠φ = 360° * sinα

Используя данный нам ∠φ (угол развертки боковой поверхности) найдем sinα

120° = 360° * sinα

sinα = 1/3

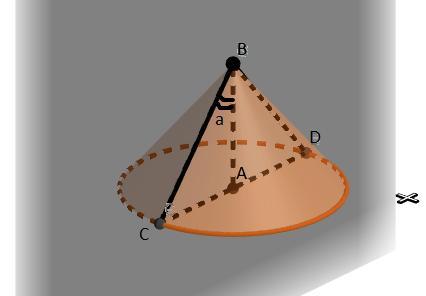
Вернемся к нашему конусу. Рассмотрим треугольник BDC.

Р ▲BDC = 24 см

ВА=АD

СА = 2R

Р ▲BDC = 2l + 2R

24 = 2l + 2R    / 2

12 = l + R

l = 12 - R

Перейдем к прямоугольному треугольнику АВС. ∠ВАС = 90°, АС - R.

АС = 12 - R

sinα = AC/CB = R/(12 - R)

R/(12 - R) = 1/3

3R = 12 - R

4R = 12

R = 3 (см)

l = 12 - 3 = 9 (см)

S(полн п-ти) = Sбок + Sосн

S(полн п-ти) = пR² + пRl

S = п3² + п * 3 * 9 = 9п + 27п = 36п