Предмет: Алгебра,
автор: krasotkanastya2000
Помогите, пожалуйста, решить дифференциальное уравнение
Приложения:
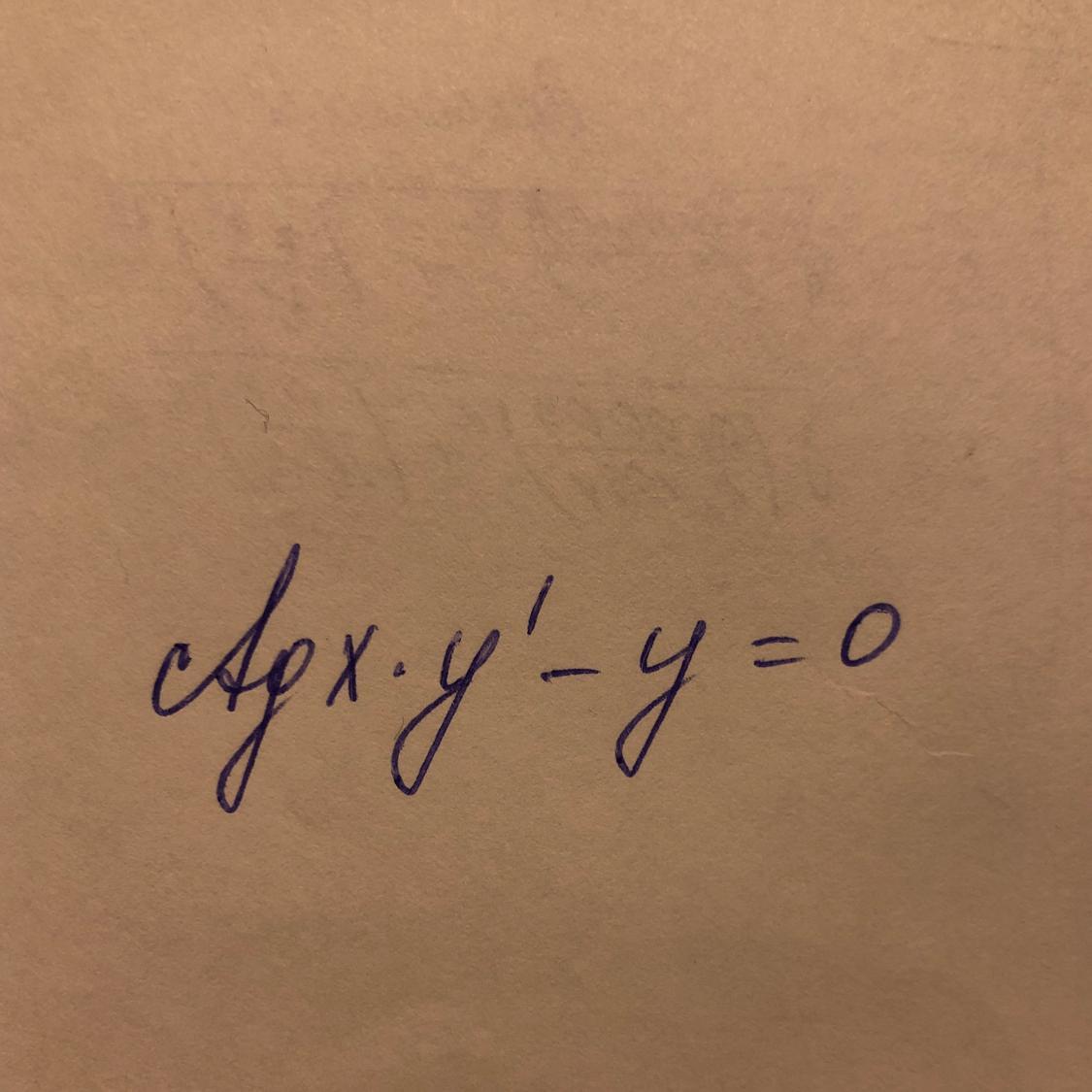
Ответы
Автор ответа:
1
Ответ:
Объяснение:
проинтегрируемобе части:
при условии, что y>0 и
Похожие вопросы
Предмет: Математика,
автор: xyhcxbbxhf
Предмет: Геометрия,
автор: Аноним
Предмет: Русский язык,
автор: poli3147
Предмет: Алгебра,
автор: svetasu
Предмет: Алгебра,
автор: PlexFX