Предмет: Геометрия,
автор: coldZero14
1. Отрезок FH перпендикулярен плоскости равнобедренного ΔHRM (HR=HM).
а) Через точку F проведите перпендикуляр к прямой RM.
б) Найдите расстояние от точки F до прямой RM, если FH = 16 см, HM = 13 см, RM = 10 см.
Ответы
Автор ответа:
9
Ответ:
FK = 20 см
Объяснение:
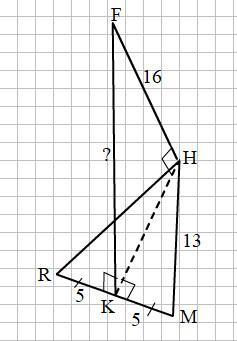
Смотри прикреплённый рисунок.
Построим НК - медиану равнобедренного ΔHRM. Тогда MK = RK = 5 см. По свойству медианы равнобедренного треугольника НК является также и высотой, то есть НК ⊥ RM.
По теореме Пифагора найдём НК:
НМ² = МК² + НК²
13² = 5² + НК²
169 = 25 + НК²
НК² = 144
НК = 12 (см)
Соединим точку F с точкой К, отрезок FK является расстоянием от F до RK. Докажем это.
FH ⊥ пл-ти НRM ⇒ FH ⊥HK и тогда НК является проекцией FK на пл-ть НRM. ПО теореме о трёх перпендикулярах: если RM ⊥ HK (проекции), то RM ⊥ FK (наклонной). Таки образом, FK ⊥RM и есть расстояние от точки F до прямой RM.
По теореме Пифагора: FK² = FH² + HK²
FK² = 16² + 12²
FK² = 400
FK = 20 (см)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: akoval23052012
Предмет: Биология,
автор: gutkannikagmailcom
Предмет: География,
автор: tarasenkomilana02
Предмет: Математика,
автор: мария1780