Question

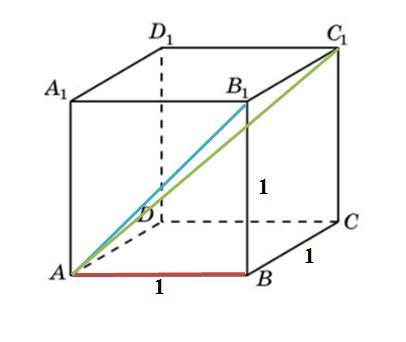
Найдите следующую длину векторов в единичном Кубе ABCDA1B1C1D1: а) АВ; б) АВ1 ; б) АС1 .​

Answer 1

Ответ:

а) АВ=1; б) $AB_{1} =\sqrt{2}$ ; в) $AC_{1}=\sqrt{3}$ .​

Пошаговое объяснение:

В единичном кубе ABCDA₁B₁C₁D₁ (см. рисунок) все ребра равны 1, то есть

AB=AD=AA₁=B₁B=B₁A₁=B₁C₁=CB=CD=CC₁=D₁D=D₁A₁=D₁C₁=1.

Отсюда а) АВ=1.

Так как вершины ABB₁ образуют прямоугольный треугольник с прямым углом в вершине B, то по теореме Пифагора

AB₁²=AB²+BB₁²=1²+1²=1+1=2.

Отсюда б) $AB_{1}=\sqrt{2}$ .

Теперь, вершины AB₁C₁ образуют прямоугольный треугольник с прямым углом в вершине B₁, то по теореме Пифагора

$\displaystyle AC_{1}^{2} =AB_{1}^{2} + B_{1}C_{1}^{2} =(\sqrt{2}) ^{2}+1^{2}=2+1=3$.

Отсюда в) $AC_{1}=\sqrt{3}$ .