Предмет: Математика,
автор: yurram905
исследовать на сходимость ряда
Приложения:
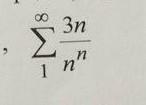
igorShap:
Вы в комментах писали про 3^n/n^n. На фото 3n/n^n. Чему верить?
Ответы
Автор ответа:
1
Тогда ряд сходится по признаку Коши
огромное спасибо братан. ты очень выручил
Похожие вопросы
Предмет: Алгебра,
автор: nekitka300
Предмет: Химия,
автор: yulichkaaa47
Предмет: Биология,
автор: nastay231020
Предмет: Математика,
автор: 1939145
Предмет: Математика,
автор: Marypul