Предмет: Математика,
автор: yurram905
исследовать на сходимость ряда (-1)^n+1×1/ n^1/2. n в корне, просто незнаю как записать пишу так: n^1/2
Приложения:
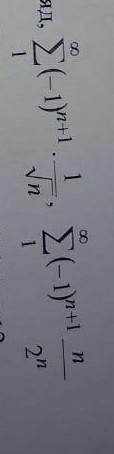
Ответы
Автор ответа:
1
1)
2) , а значит функция
монотонно убывает. Тогда
3)
Тогда ряд сходится по признаку Лейбница
yurram905:
А он сходится абсолютно или условно?
Условно. И это уже исследование на абсолютную сходимость. Оно здесь просто по степенному признаку идёт
ряд сходится условно, потому что 1/n^½ это обобщенный гармоничнский ряд, и данный ряд расходится
поэтому?
то есть предел 1/n^½ равен нулю, но сам 1/n^½ является обобщенным гармоническим рядом, который расходится
поэтому ряд сходится условно
я правильно понял?
Обобщённым гармоническим рядом с k=1/2≤1, просто сказать про гармонический недостаточно
все
ок
Похожие вопросы
Предмет: Математика,
автор: zholodenkodiana
Предмет: Геометрия,
автор: babicaroslav121
Предмет: Геометрия,
автор: Svetkakrw
Предмет: География,
автор: кисуля60
Предмет: Биология,
автор: Shoshina1