Предмет: Алгебра,
автор: danilarutyunov37
Упростите выражения:
Приложения:
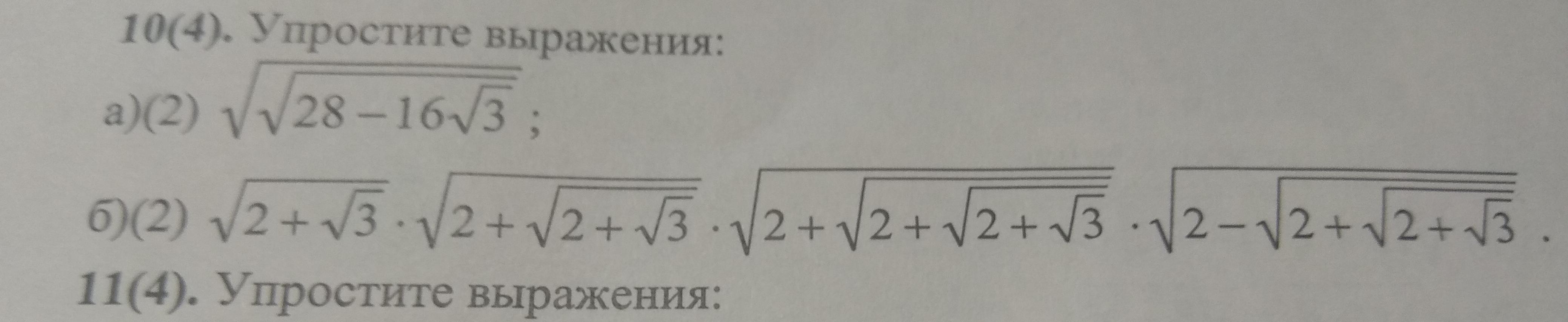
Ответы
Автор ответа:
2
1)
2)
danilarutyunov37:
Спасибо. А ещё поможешь?
Похожие вопросы
Предмет: Алгебра,
автор: mars82
Предмет: Русский язык,
автор: wwfotosh
Предмет: ОБЖ,
автор: typou1191
Предмет: Алгебра,
автор: Лёлька17x
Предмет: История,
автор: voronkovavaleriя