Question

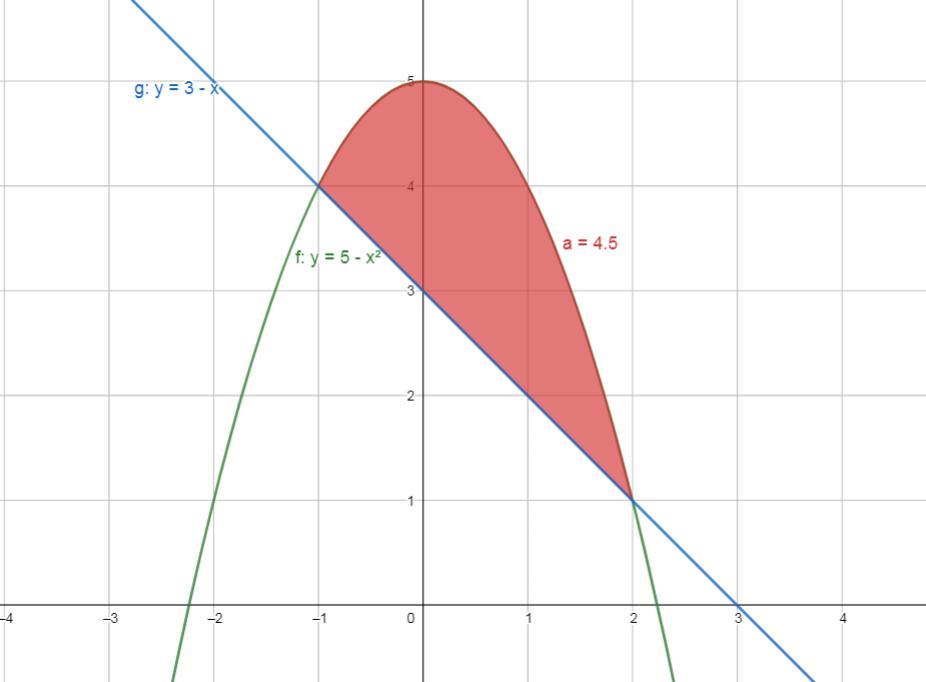
знайдіть площу фігури, обмеженної лініями: y=5-x², y=3-x
Очень срочно!! пожалуйста​

Answer 1

Ответ: 4,5 (ед)²

Объяснение:

Находим точки пересечения графиков

y = 5 - x²  ,  y = 3 - x

5 - x²  = 3 - x

x² -x -2  =0

( x + 1 )( x - 2 ) =0  

x₁  = - 1 ;  x₂  = 2

Находим определенный интеграл

$\displaystyle \int\limits^a_b {(5-x^2 -(3-x) )} \, dx \int\limits^2_{-1}(- x^2 +x +2) \, dx = \left (-\frac{x^3}{3} +\frac{x^2}{2} + 2x \right )~ \Bigg | ^{2} _{-1} = \\\\\\= -\frac{8}{3} +\frac{4}{2} + 4 - \bigg( \frac{1}{3} + \frac{1}{2} -2 \bigg) =- \frac{9}{3} + 8 - 0,5 = -3,5 + 8 = 4,5$