Предмет: Геометрия, автор: Kat14z

ПОМОГИТЕ ПОЖАЛУЙСТА! Объем треугольной пирамиды SABC равен 35. Плоскость проходит через сторону AB основания этой пирамиды и пересекает ребро SC в точке D, которая делит его в отношении 2:5, считая от вершины S. Найдите объем пирамиды DABC. ДАМ 60 БАЛЛОВ.

Ответы

Автор ответа: Hrisula

Ответ: V(DABC)=25 (ед. объема) Объемы пирамид с общим основанием пропорциональны проведенным к нему высотам.

Объяснение:

Формула объема пирамиды

V=S•h:3. где S - площадь основания пирамиды, h - ее высота.

V(SABC)=S(ABC)•SO:3

Основание исходной пирамиды и полученной сечением общее.

Поэтому объем DABC=S(ABC)•DH:3, здесь DH- высота пирамиды DABC, опущенная из вершины D на плоскость основания.

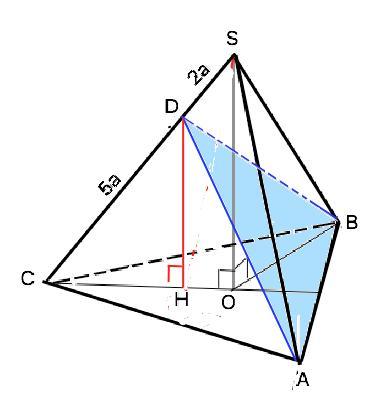
Рассмотрим ∆ ЅСО. Перпендикуляр DН параллелен перпендикуляру ЅО ( высоте пирамиды). Прямоугольные треугольники ЅСО и DCO подобны по общему острому углу.

k=DC:SC =5a:(2a+5a)=5/7 =>

V1(DABC)=S(ABC)•(5/7)•SO:3 откуда

V1=(5/7)V(SABC)=35•5/7=25 (ед. объема)

Приложения: