Приблизительно рассчитать с помощью дифференциала
а) (4,01)^1,5; б) lg(1,5);
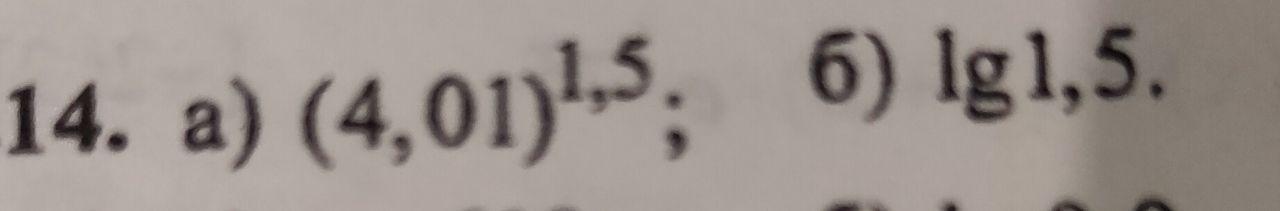
Ответы
Ответ:
Пошаговое объяснение: а) ≈8,03; б) ≈0,217.
а) Рассмотрим функцию y=x^1,5. Её значение в точке x0=4 находится легко: y(x0)=y(4)=4^1,5=8. Придадим теперь аргументу приращение Δx=0,01, тогда функция получит приращение Δy≈y'(x0)*dy=y'(x0)*dx=y'(x0)*Δx и искомое значение y(x0+Δx)≈y(x0)+dy. Производная y'(x)=1,5*√x, поэтому y'(x0)=y'(4)=3. Тогда y(4,01)≈8+3*0,01=8,03.
б) Рассмотрим функцию y=lg(x), Её значение в точке x0=1 находится легко: y(x0)=0. Придадим аргументу приращение Δx=0,5, тогда функция получит приращение Δy≈y'(x0)*dy=y'(x0)*dx=y'(x0)*Δx и тогда y(x0+Δx)≈y(x0)+dy. Производная y'(x)=1/[x*ln(10)], поэтому y'(x0)=1/ln(10). Тогда y(1,5)≈0+1/ln(10)*0,5≈0,217.
Заметим, что в этом случае вследствие большого Δx точность вычисления невелика. Это и естественно, так как точность от замены приращения функции её дифференциалом повышается с уменьшением приращения аргумента и обратно.